Develops
Here you can find the projects and developments I have been working on.
Structural Analysis
Development of finite element analysis frameworks for a wide range of structural elements, including line, plane, and solid formulations in both two- and three-dimensional domains. These frameworks support various types of analyses—such as static, dynamic, and spectral—offering versatile and reliable tools for structural engineering applications.
Fem
Program for static finite element analysis, supporting line, plane, and solid elements in both two- and three-dimensional domains. It includes multiple numerical integration schemes, ensuring accuracy and flexibility across a wide range of structural applications.

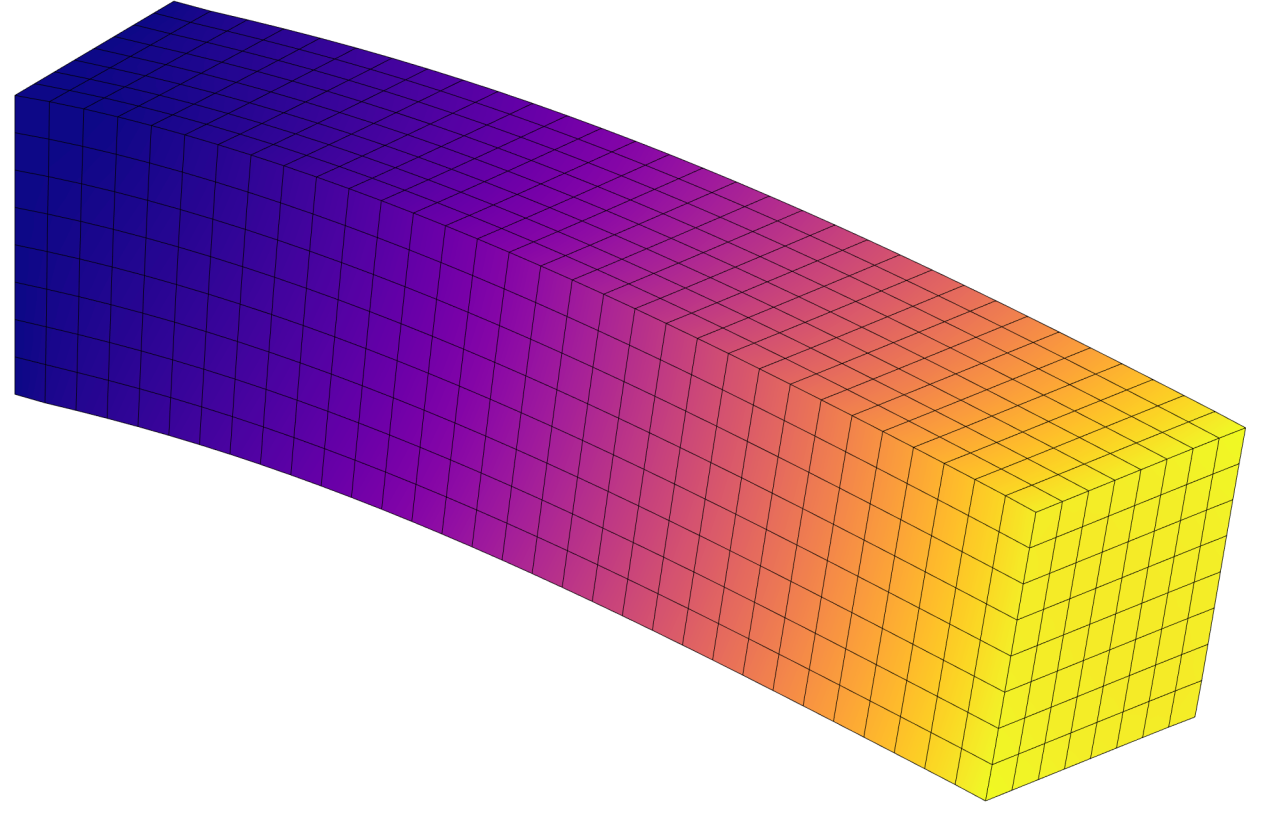
Dynamic Fem
Program for dynamic finite element analysis, incorporating various integration methods, additional mass considerations, and dynamic load functions. The program supports loading based on a general pattern, a dynamic pattern, and ground motion inputs, providing flexibility for a wide range of structural dynamic simulations.
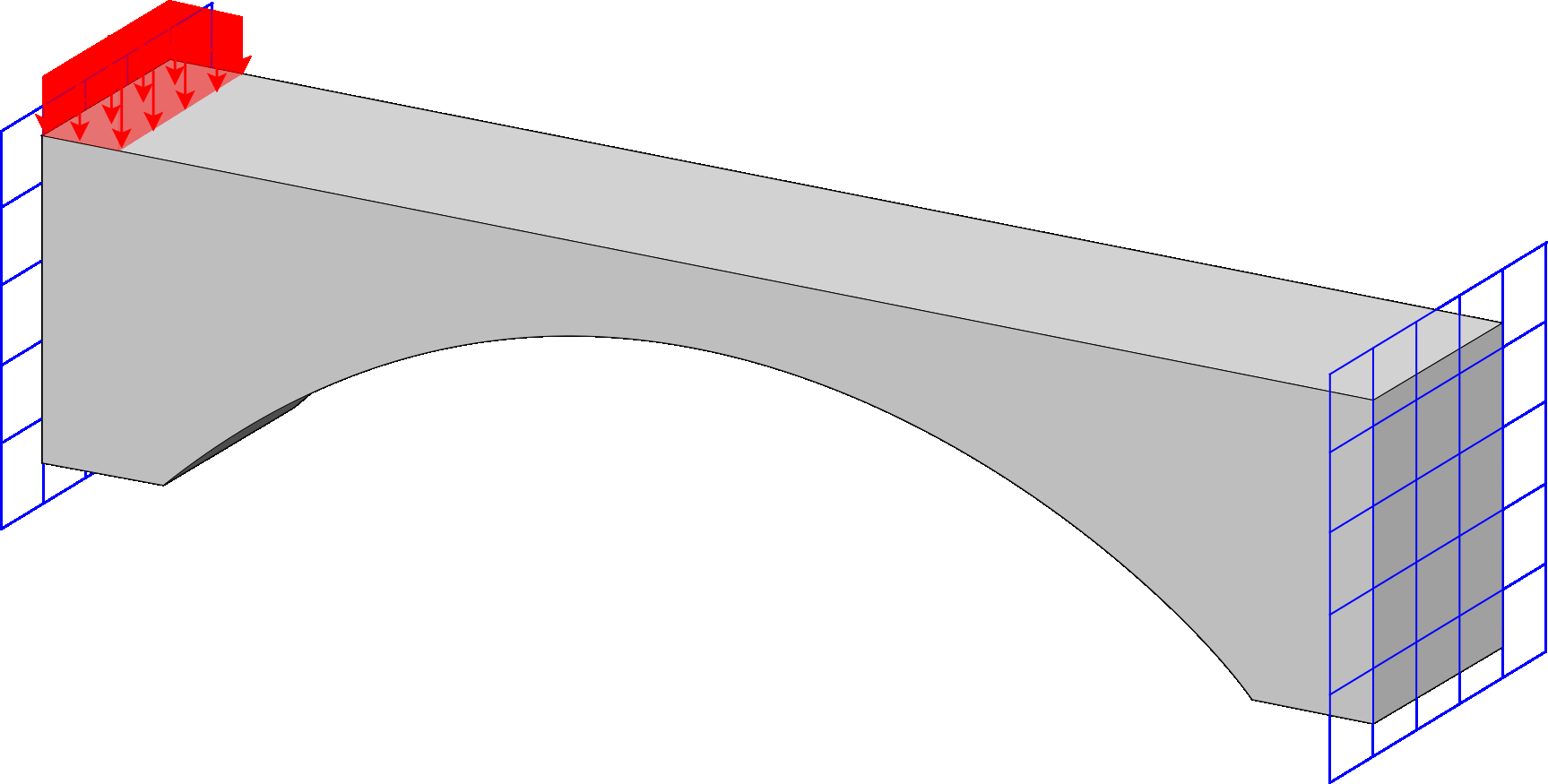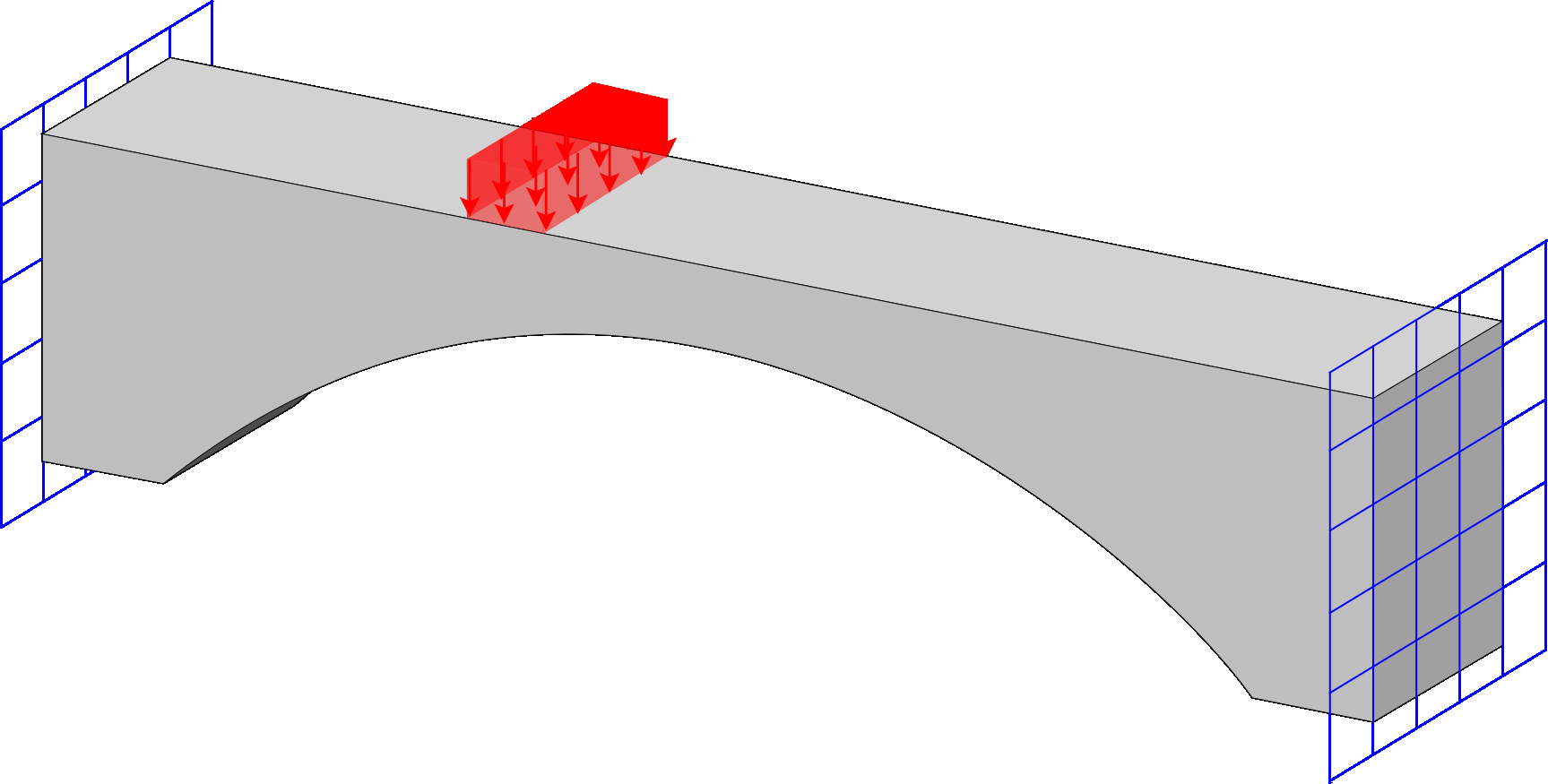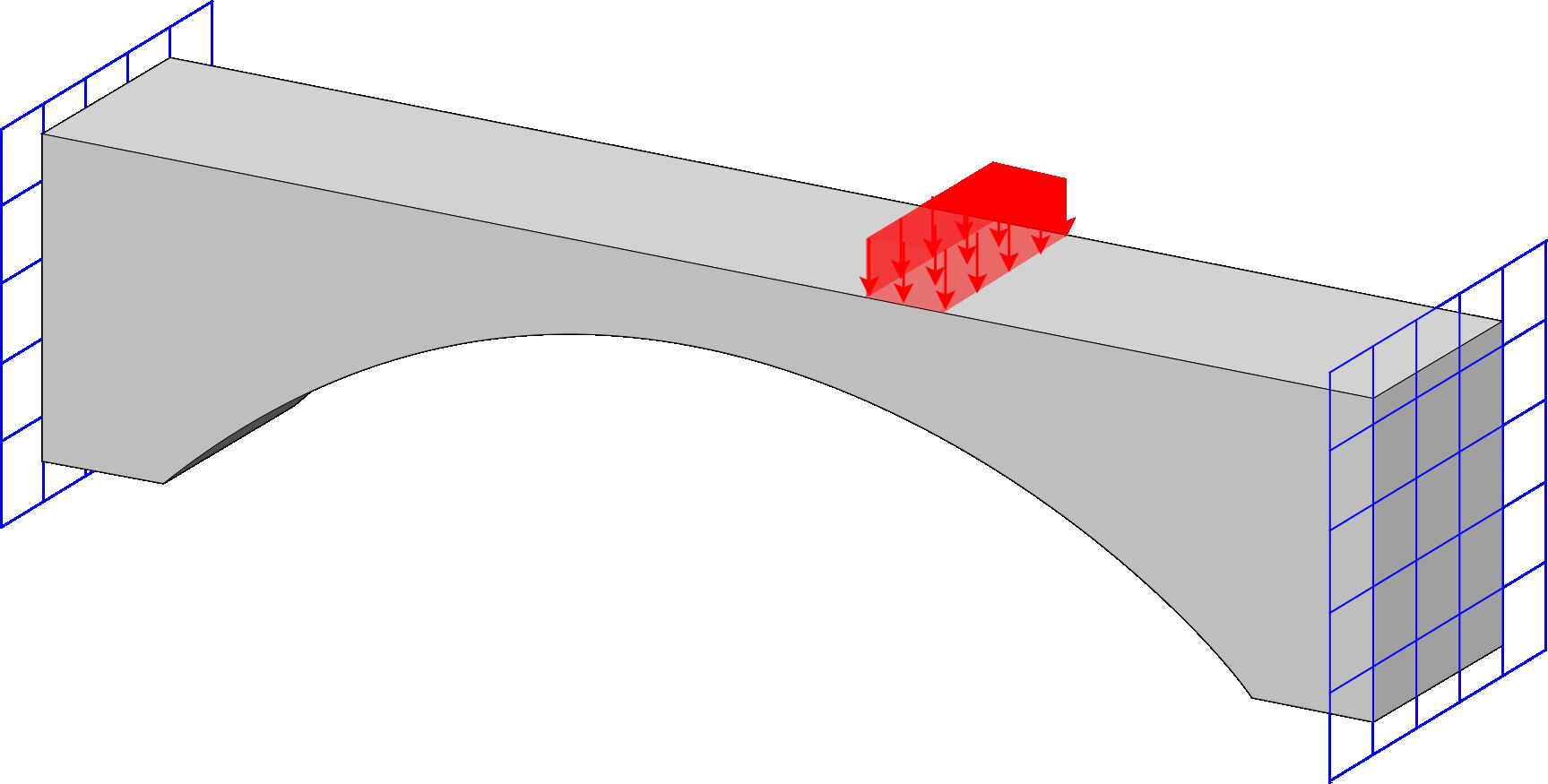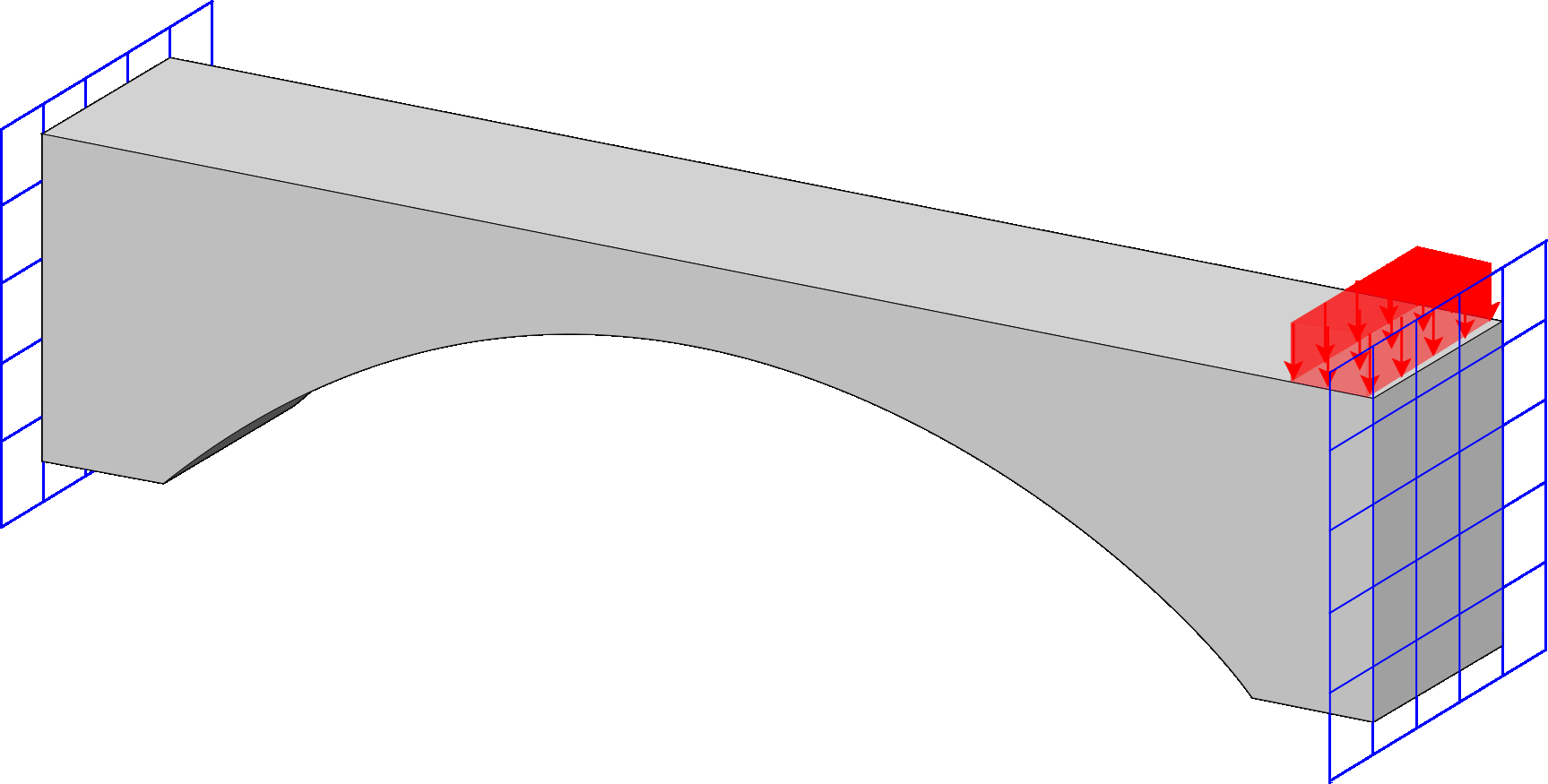

Spectrum Fem
Program for response spectrum analysis, incorporating both eigen and Ritz vectors for modal analysis. It includes multiple combination techniques for evaluating the structural response, providing accurate and flexible assessments of dynamic behavior under seismic or other time-independent loadings.
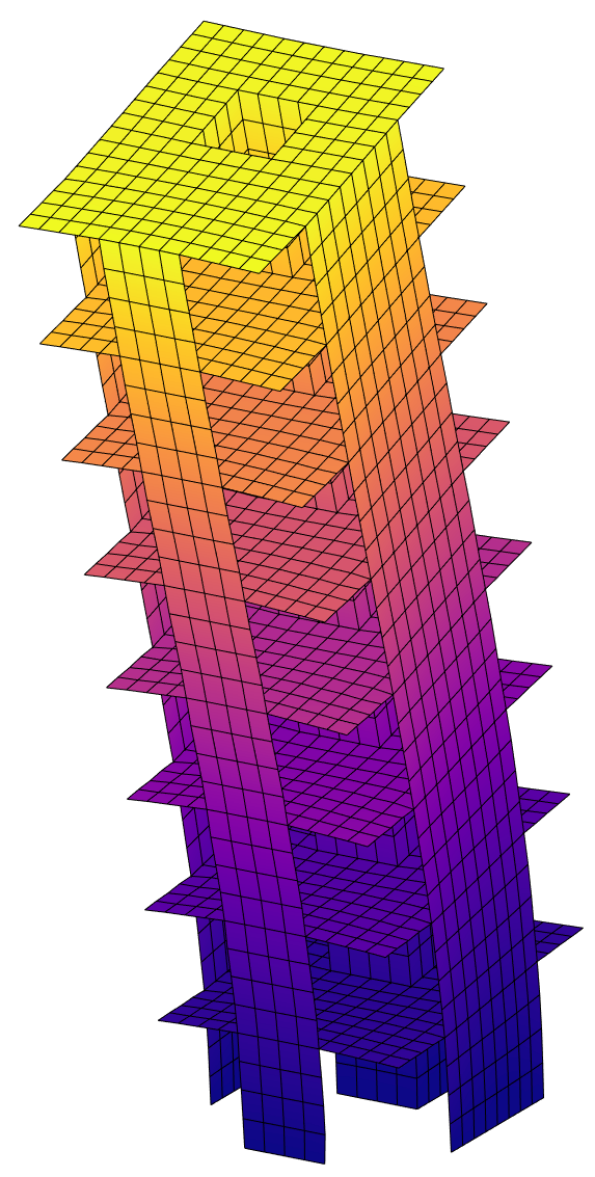
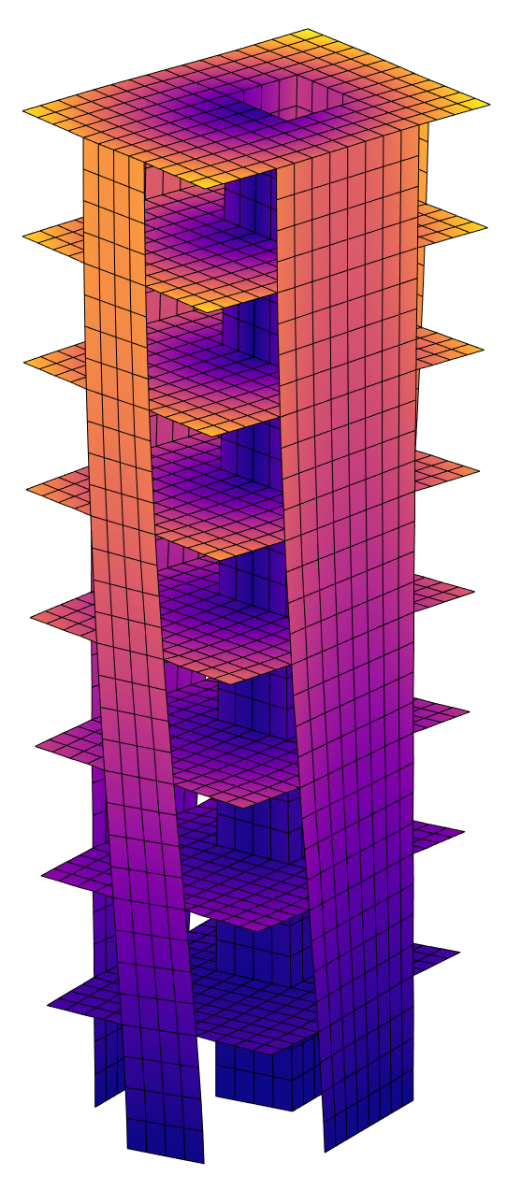
Struct Fem
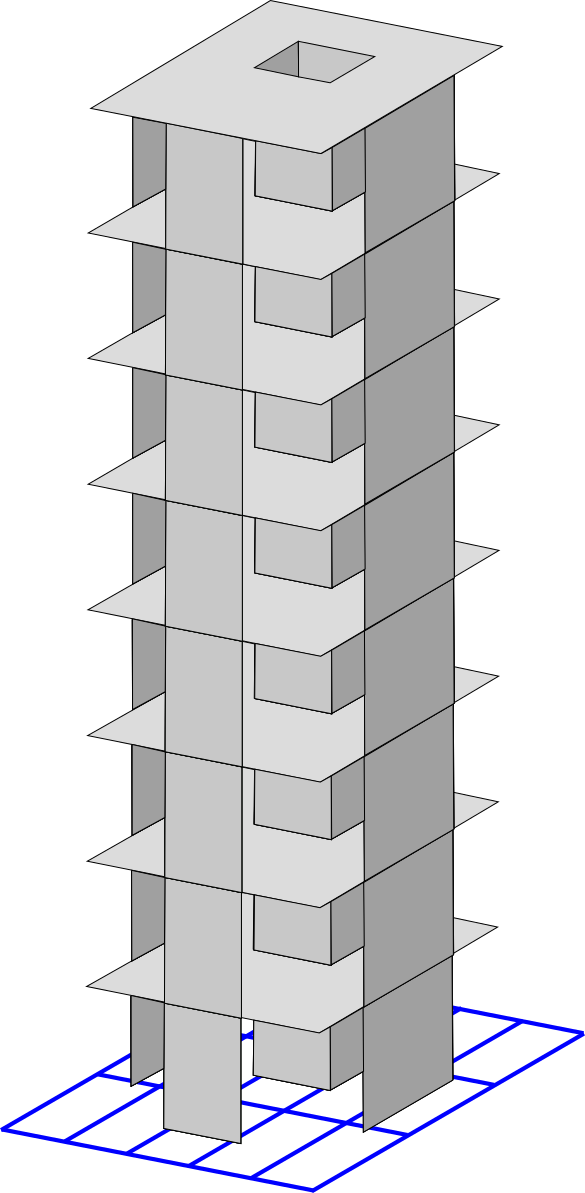
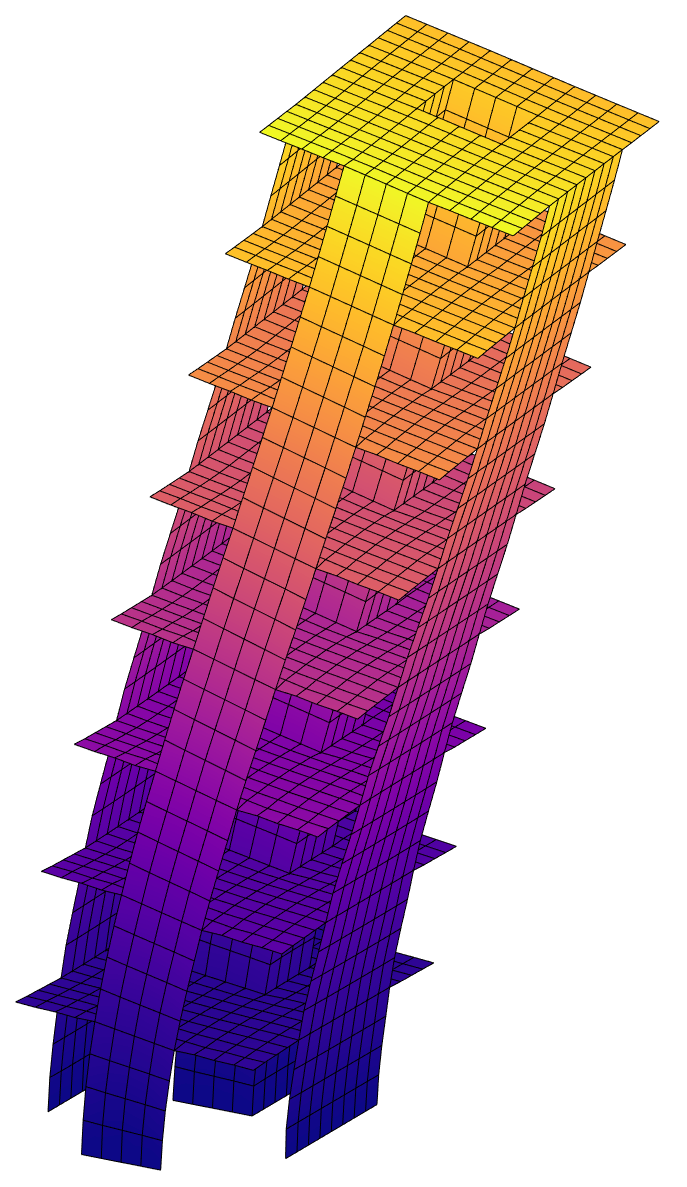
Program for multi-element static structural analysis, enabling the evaluation of structures composed of various element types. It supports the incorporation of kinematic constraints and release conditions, providing accurate modeling of complex structural systems.
Topology Optimization
Development of topology-optimization frameworks spanning diverse applications: classical topology optimization; multi-material formulations; stress-constrained optimization; optimization under dynamic loads; subdomain-selection approaches; shape optimization; and optimization for multiple load cases. These frameworks are designed to provide flexible, scalable tools for advanced structural design.
Top
Program for topology optimization, supporting alternative objectives such as compliance minimization or control-point displacement constraints. The implementation allows for different update schemes, providing flexibility and adaptability for various optimization strategies.
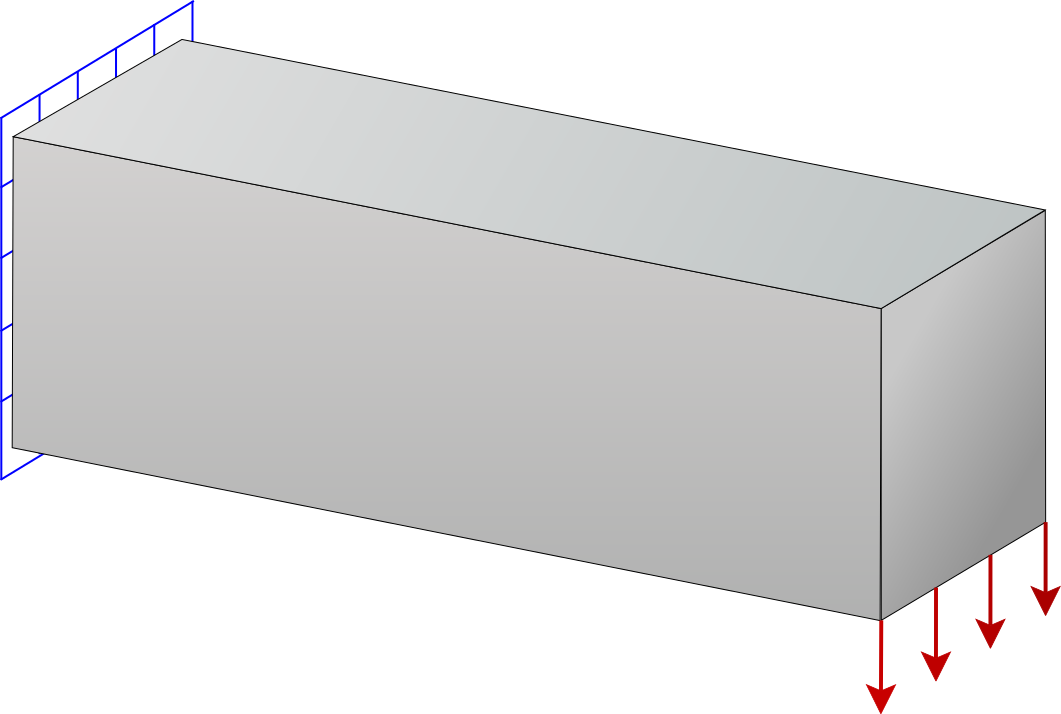

Shape Top
Program for shape optimization, built on a constrained topology-optimization framework. This approach enables shape refinement directly on the structural domain, avoiding any requirement to predefine a parametric boundary.

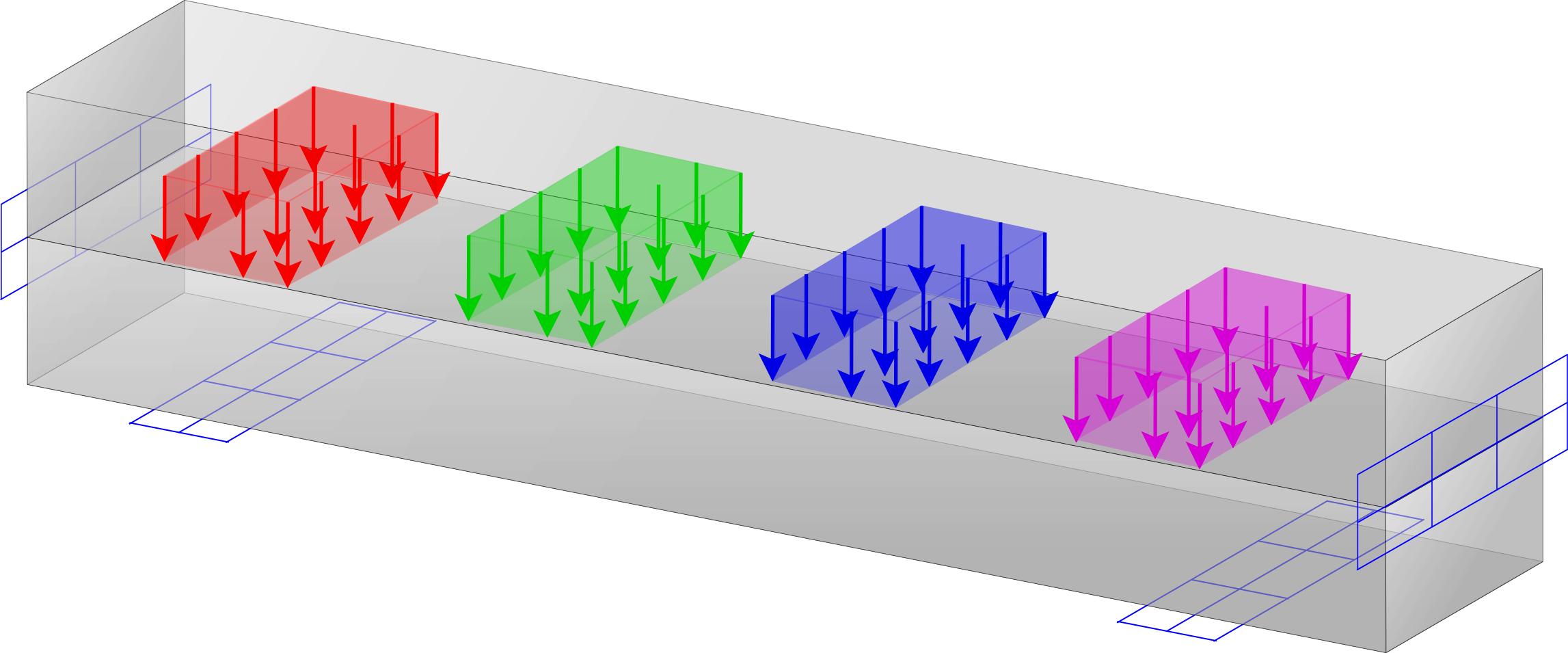
Multi Load Top
Program for multi-load topology optimization. The implementation supports different methods for handling multiple loads and also provides the possibility of defining multiple objectives for each individual load case.

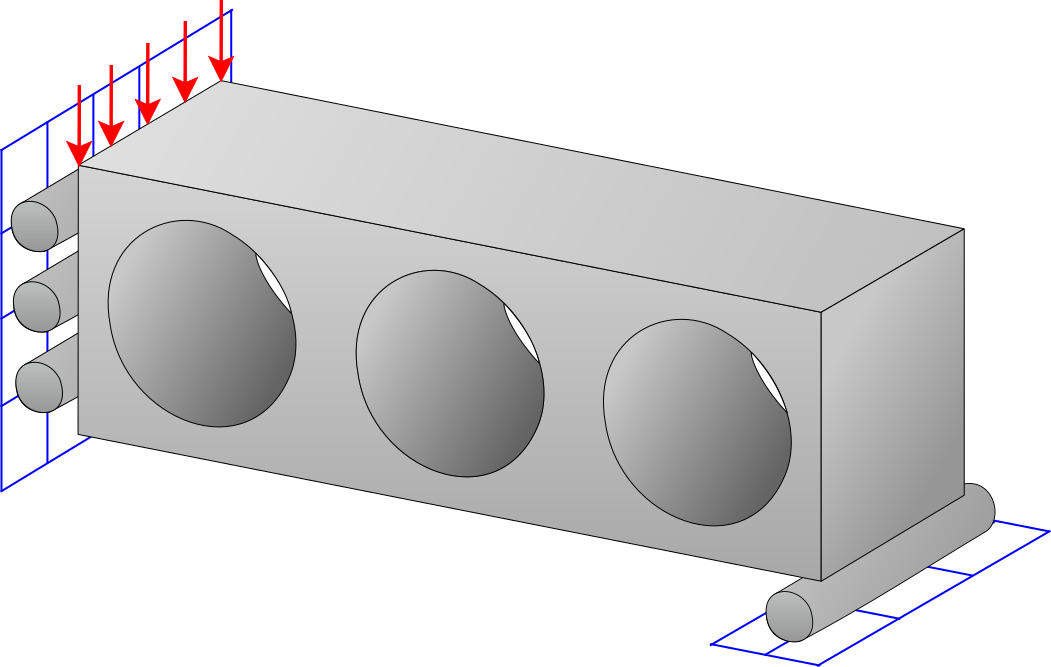
SubDomain Top
Program for topology optimization with subdomain selection. The framework enables independent control of the global volume fraction and the number of active subdomains, and supports distinct interpolation schemes for material densities as well as subdomain penalization. These features provide flexibility for designing structures with localized topology control and tailored material representations.
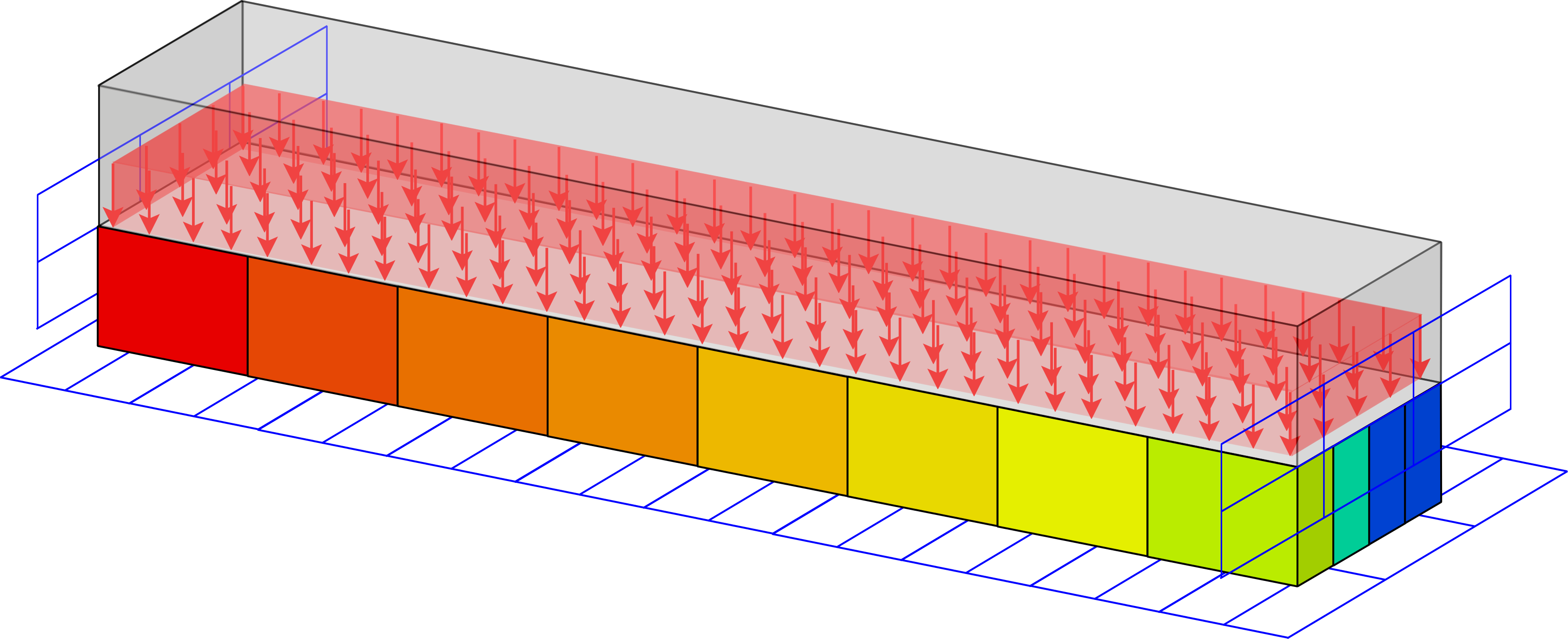

Multi Mat Top
Program for multi-material shape topology optimization. The implementation allows assigning different interpolation schemes, defining passive regions locked to a chosen material, and selecting among various update schemes, providing flexibility and control over the optimization process.

Dynamic Top
Program for dynamic topology optimization. The implementation enables topology optimization under dynamic load cases derived from static patterns, dynamic patterns, and even ground motions. The framework supports optimization in both the time and frequency domains, with multiple methods available for each approach.
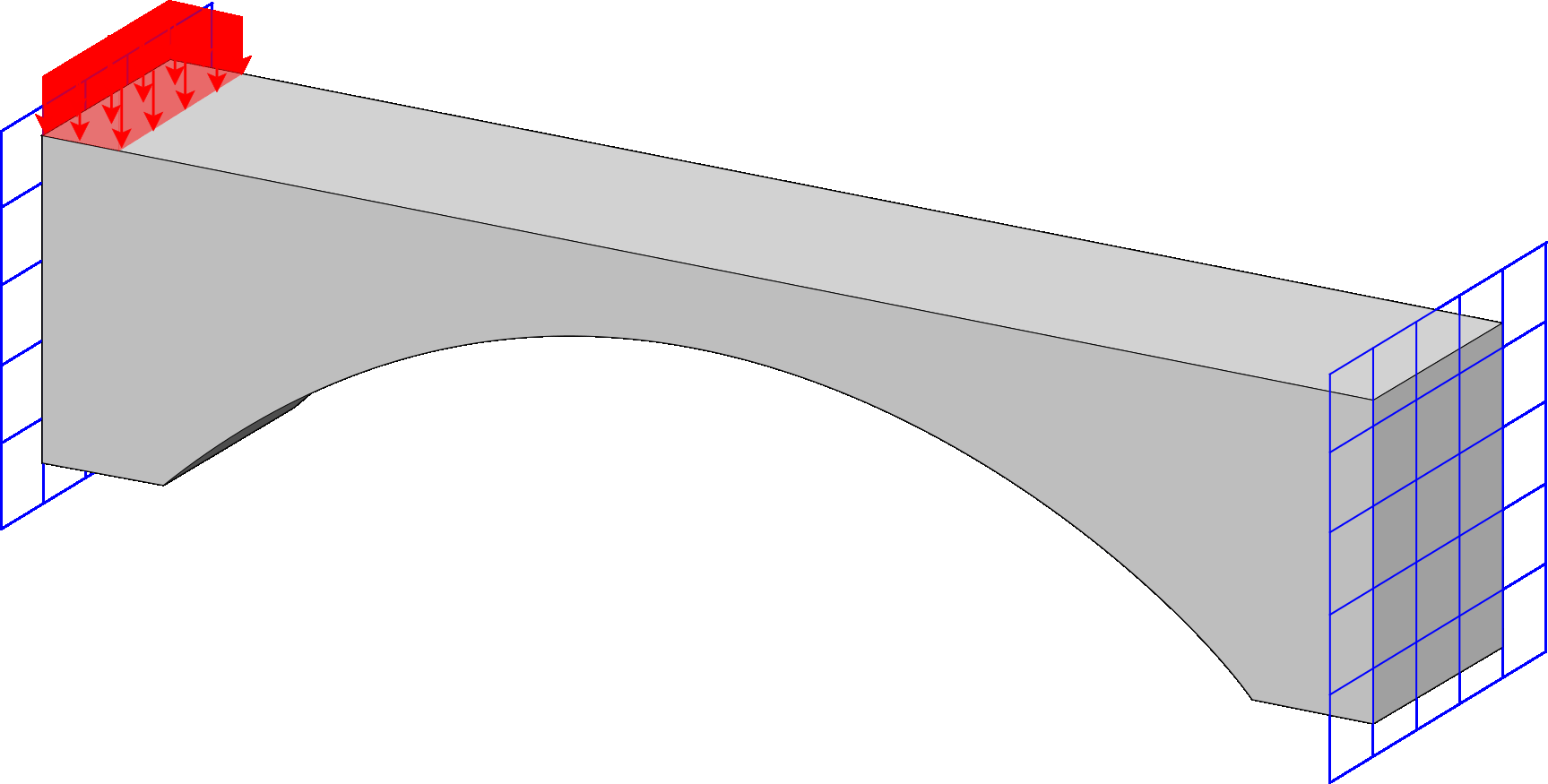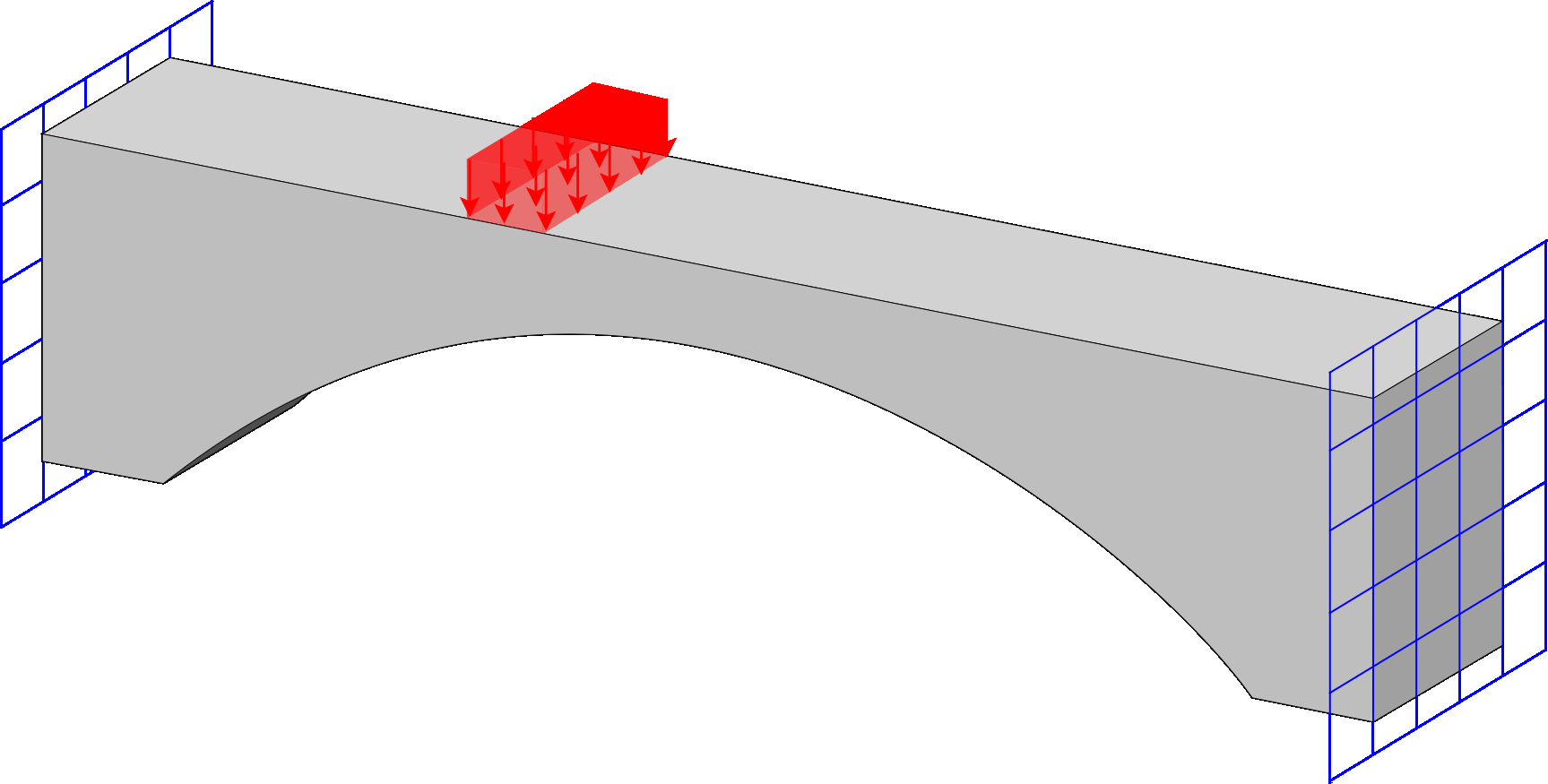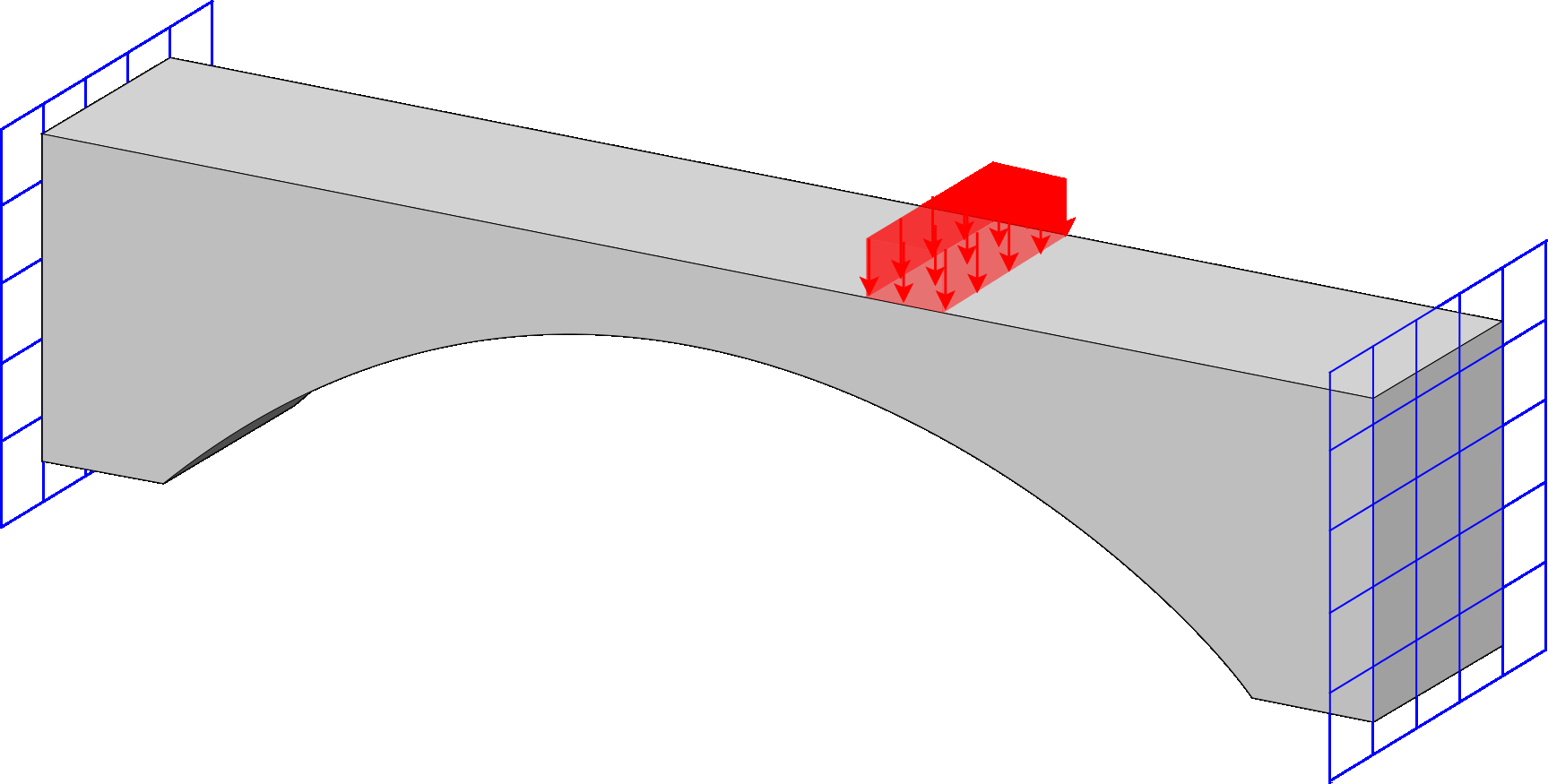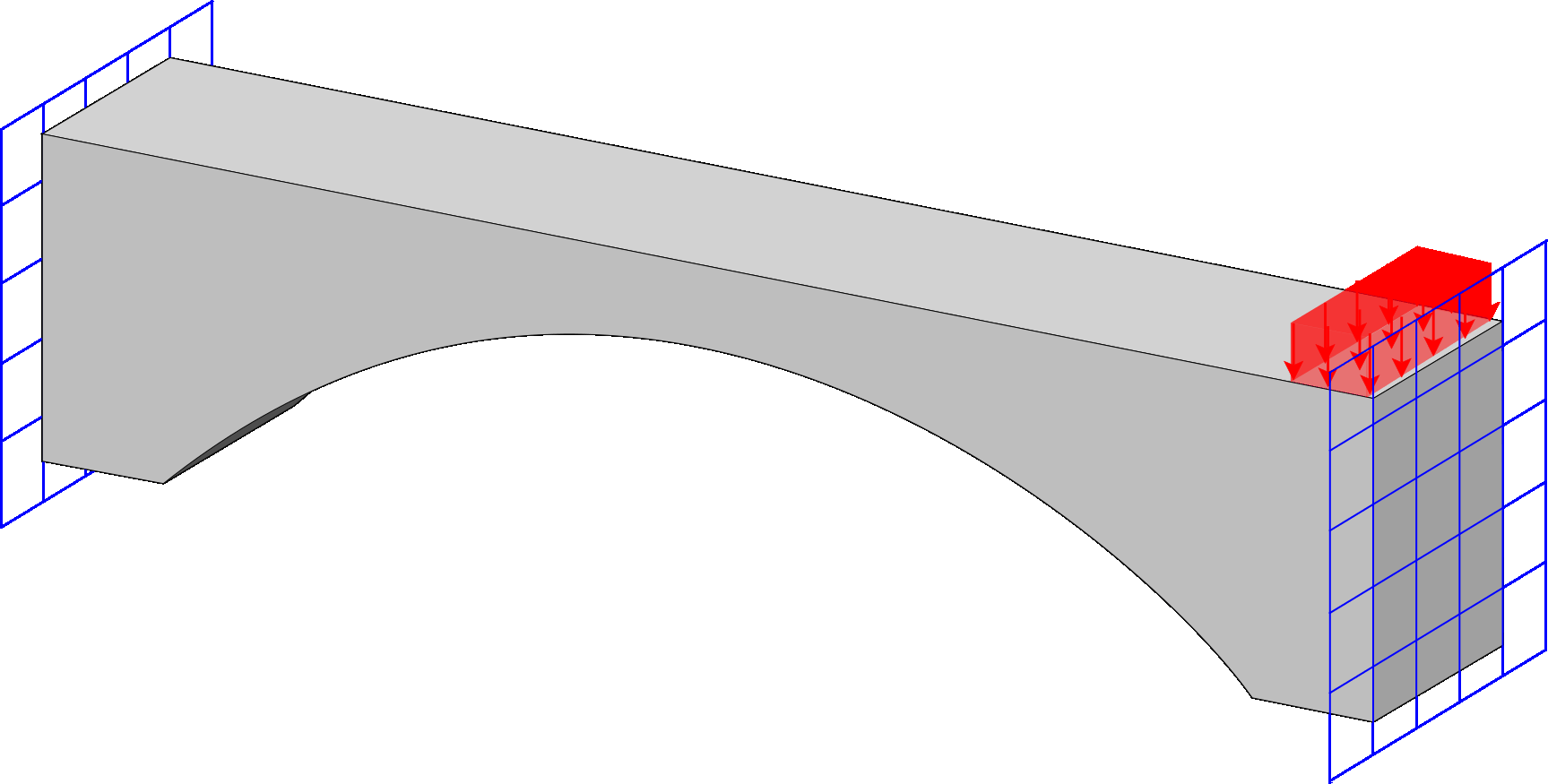

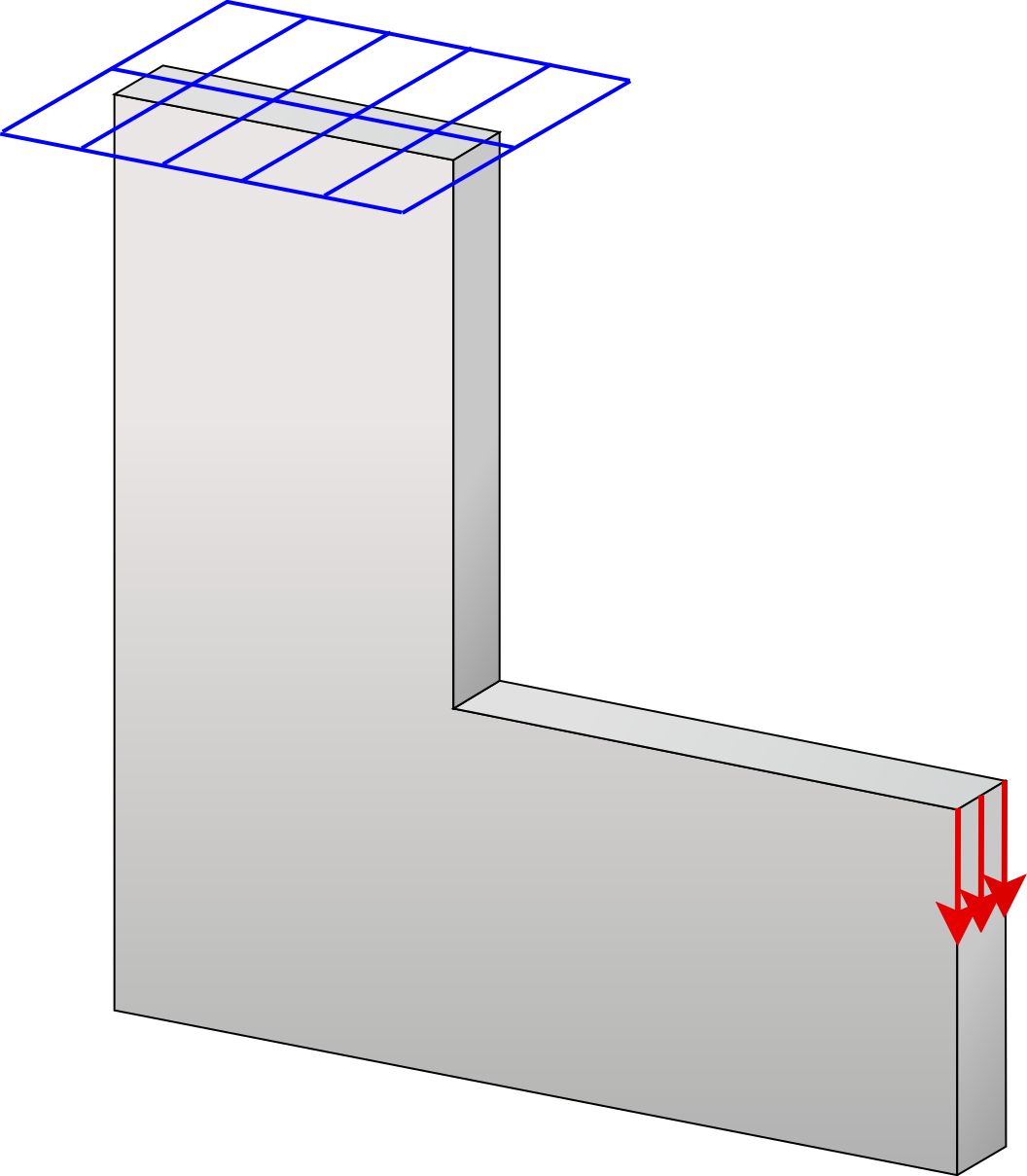
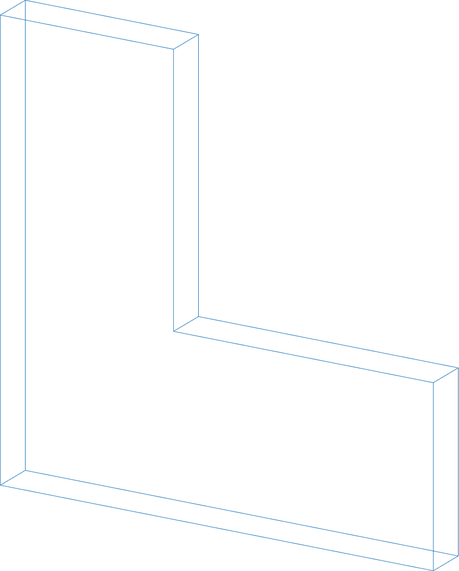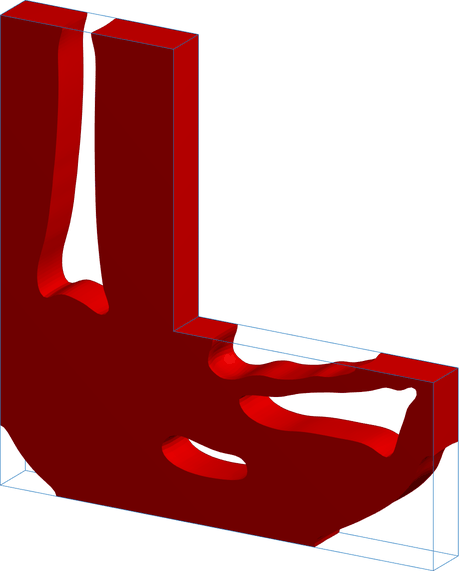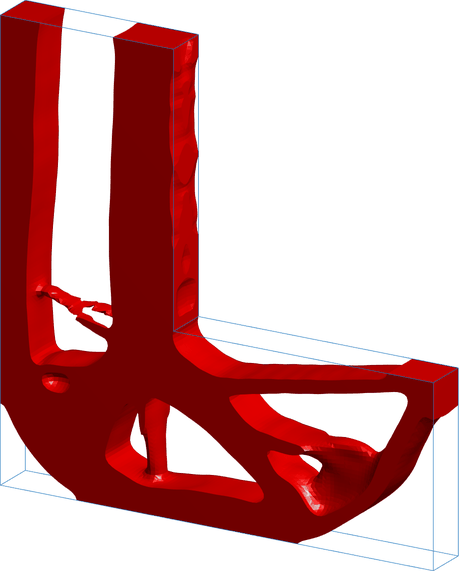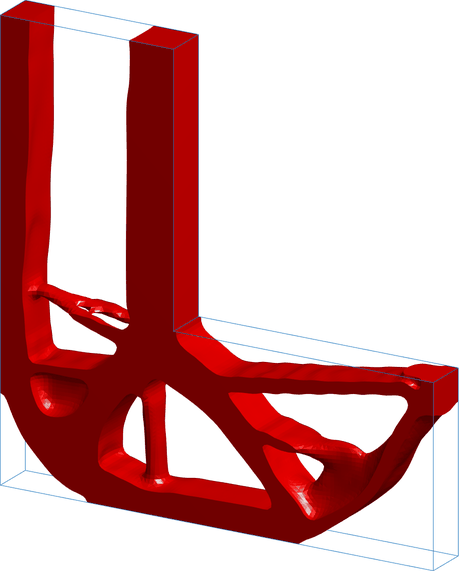
Stress Top
Program for stress-constrained topology optimization. The implementation supports different material interpolation and projection schemes, offers multiple techniques for handling vanishing constraints, and allows selection of the number of Gauss points at which stress constraints are applied.
Topology Optimization Applications
Development of topology optimization applications for real engineering problems.
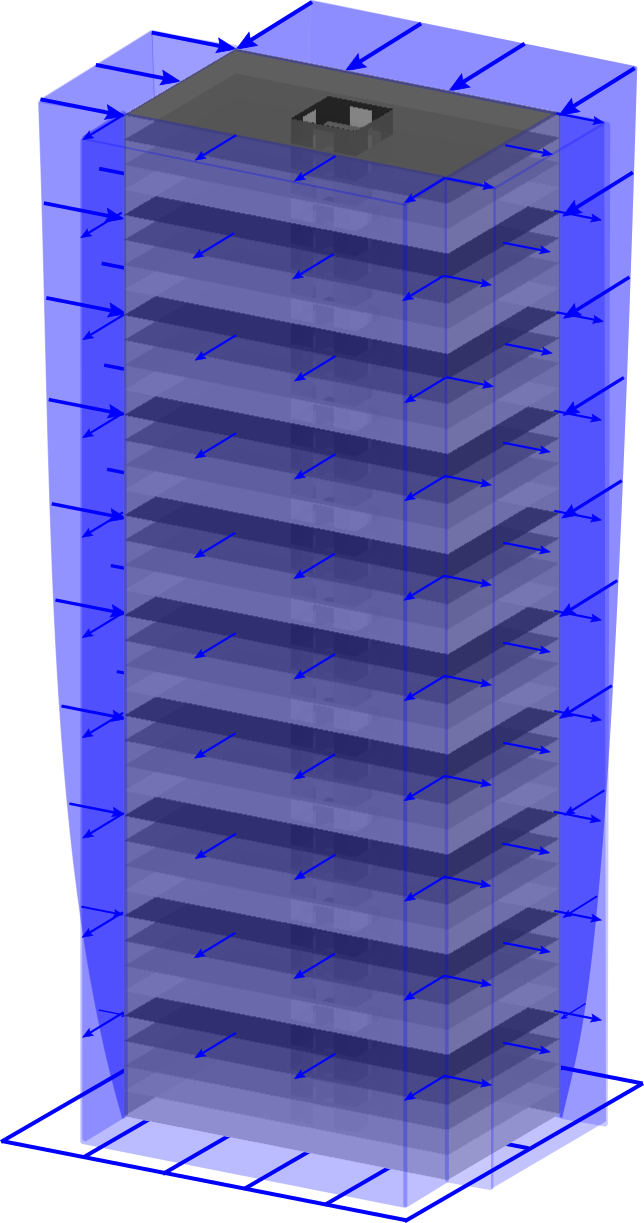
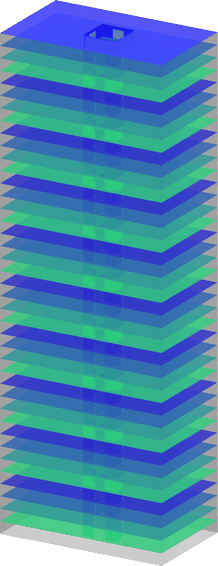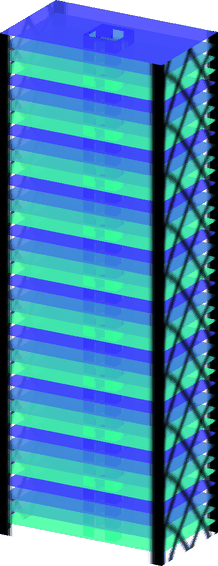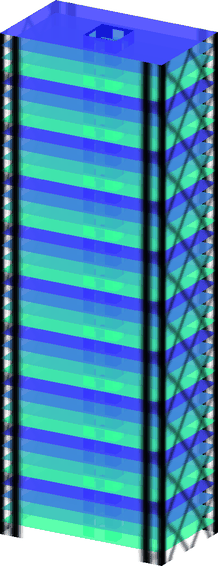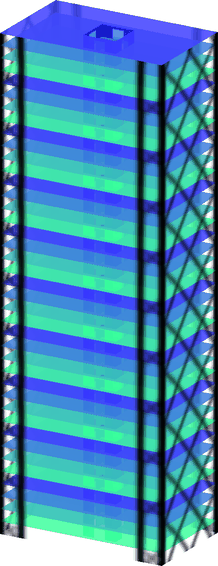
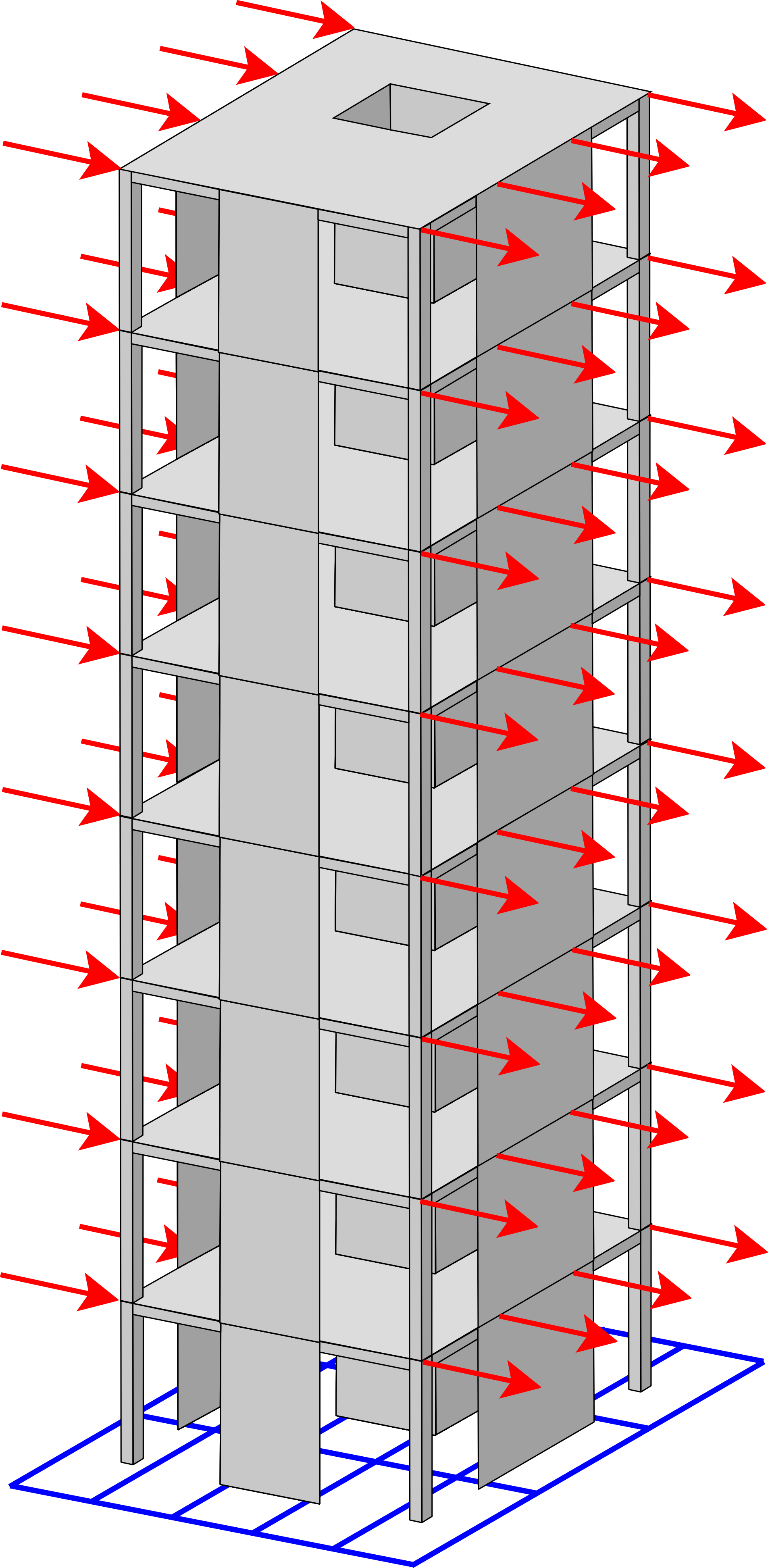
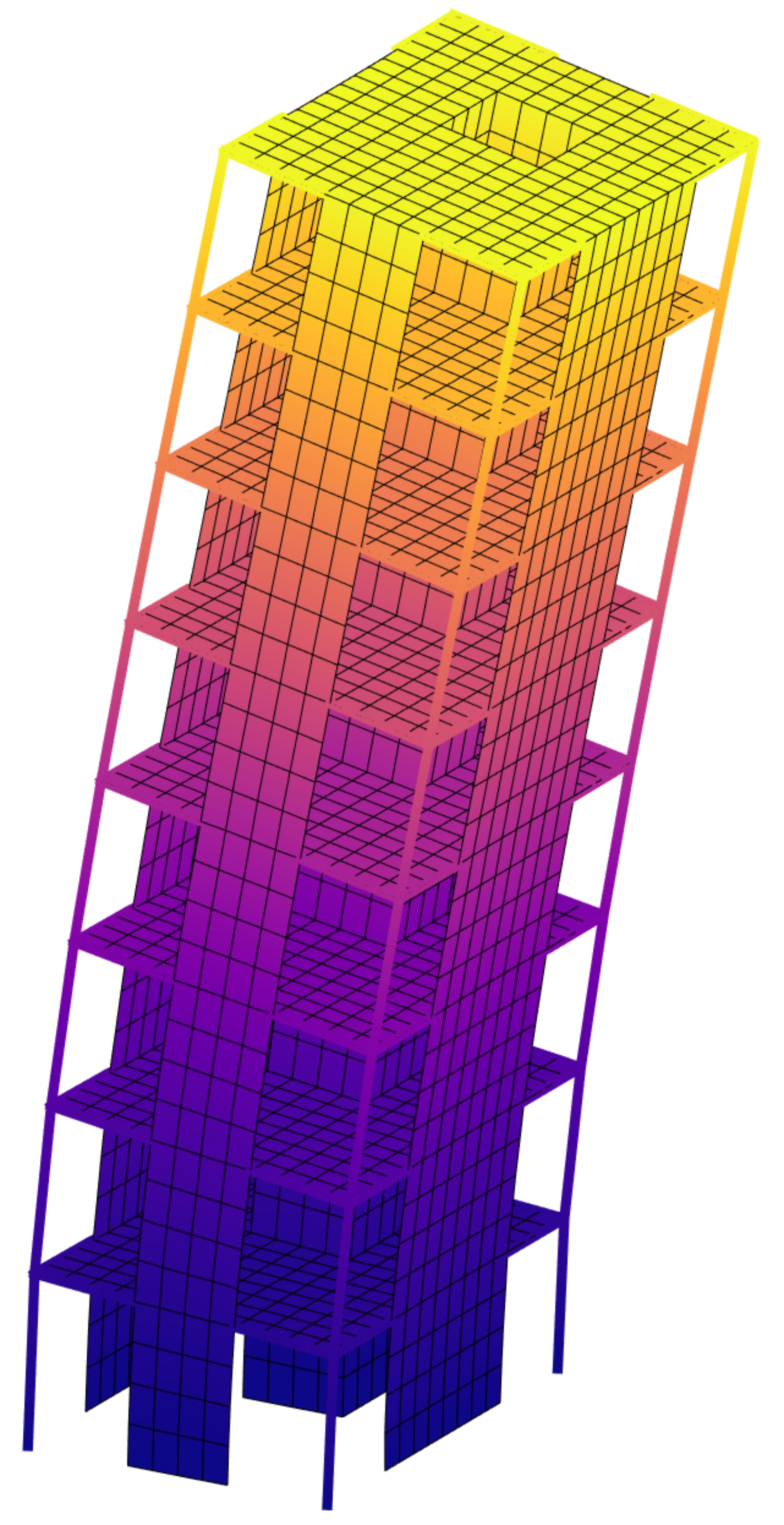
Building Wind Top
Program for topology optimization of building facades subjected to static equivalent wind loads. It includes the use of pattern repetition and multi-objective optimization techniques.