Personal Projects
This section lists some of the projects and developments I am currently working on.
Development of finite element analysis frameworks for a wide range of structural elements, including segment, plane, and solid formulations in both two- and three-dimensional domains. These frameworks support static, dynamic, and spectral analyses for structural engineering applications.
Fem
Computational framework for linear static finite element analysis, supporting plane, solid, shell, and curved-shell elements. It includes linear and quadratic element types, multiple numerical-integration schemes, various boundary conditions, and stress post-processing.

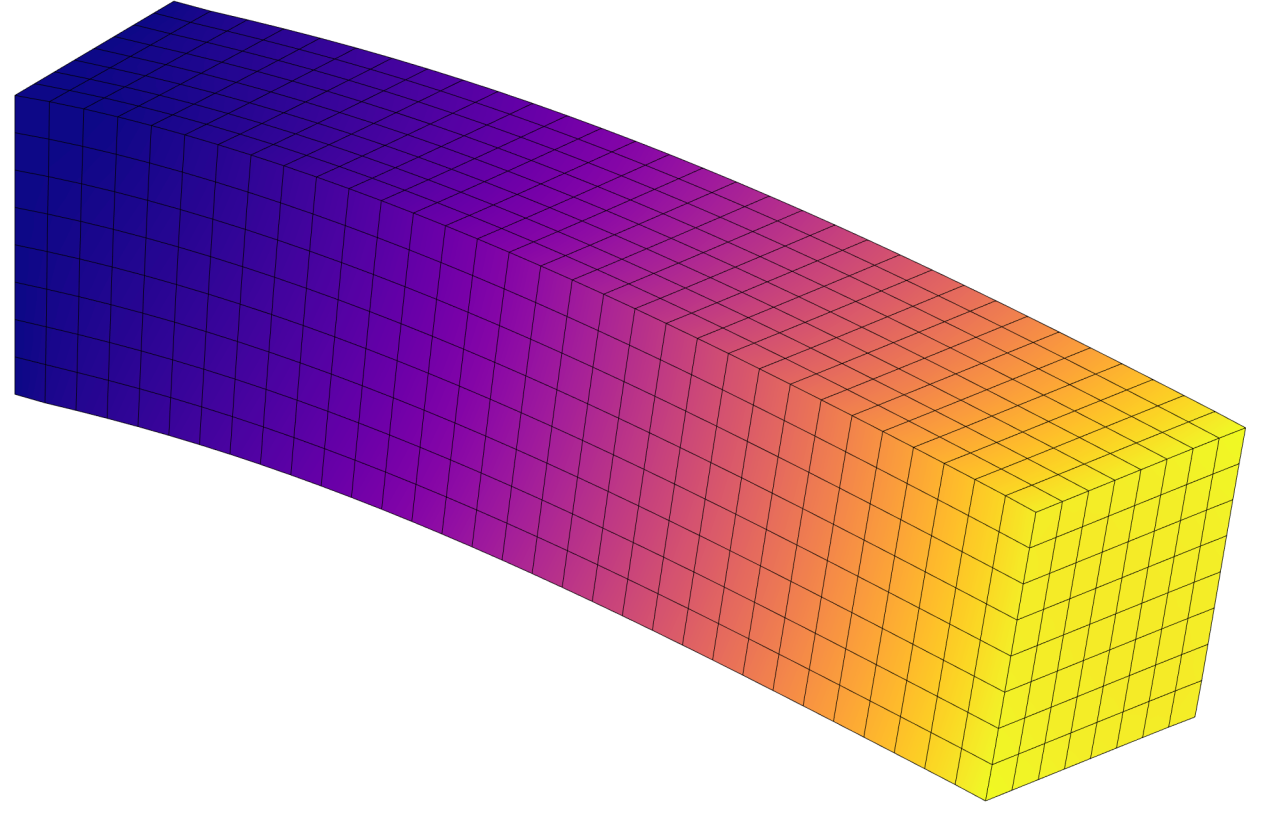
Dynamic Fem
Computational framework for dynamic finite element analysis, incorporating various integration methods, additional mass formulations, and dynamic load functions. It supports dynamic loads based on fixed patterns with varying amplitude in time, completely dynamic load patterns, and ground-motion acceleration.
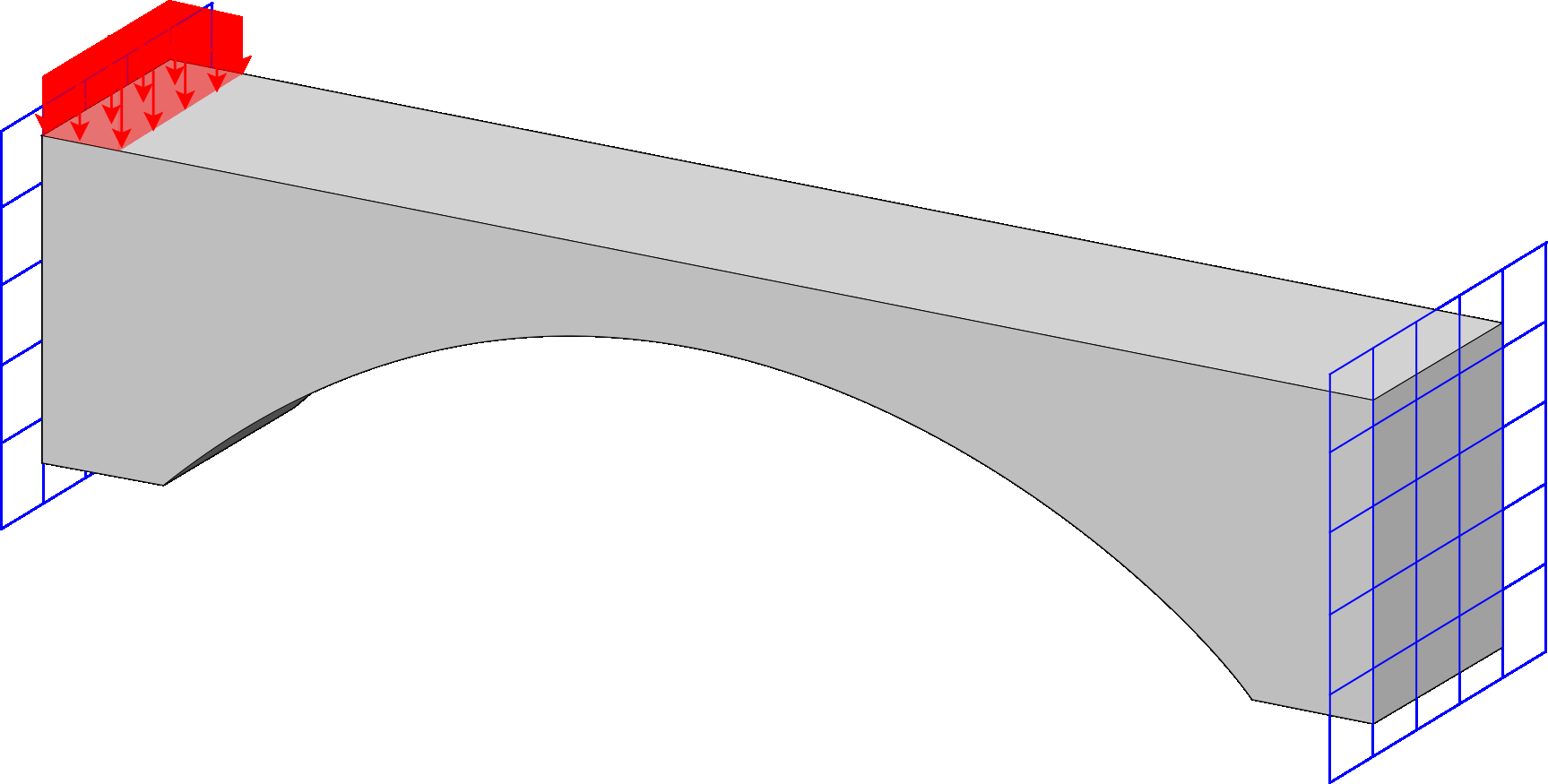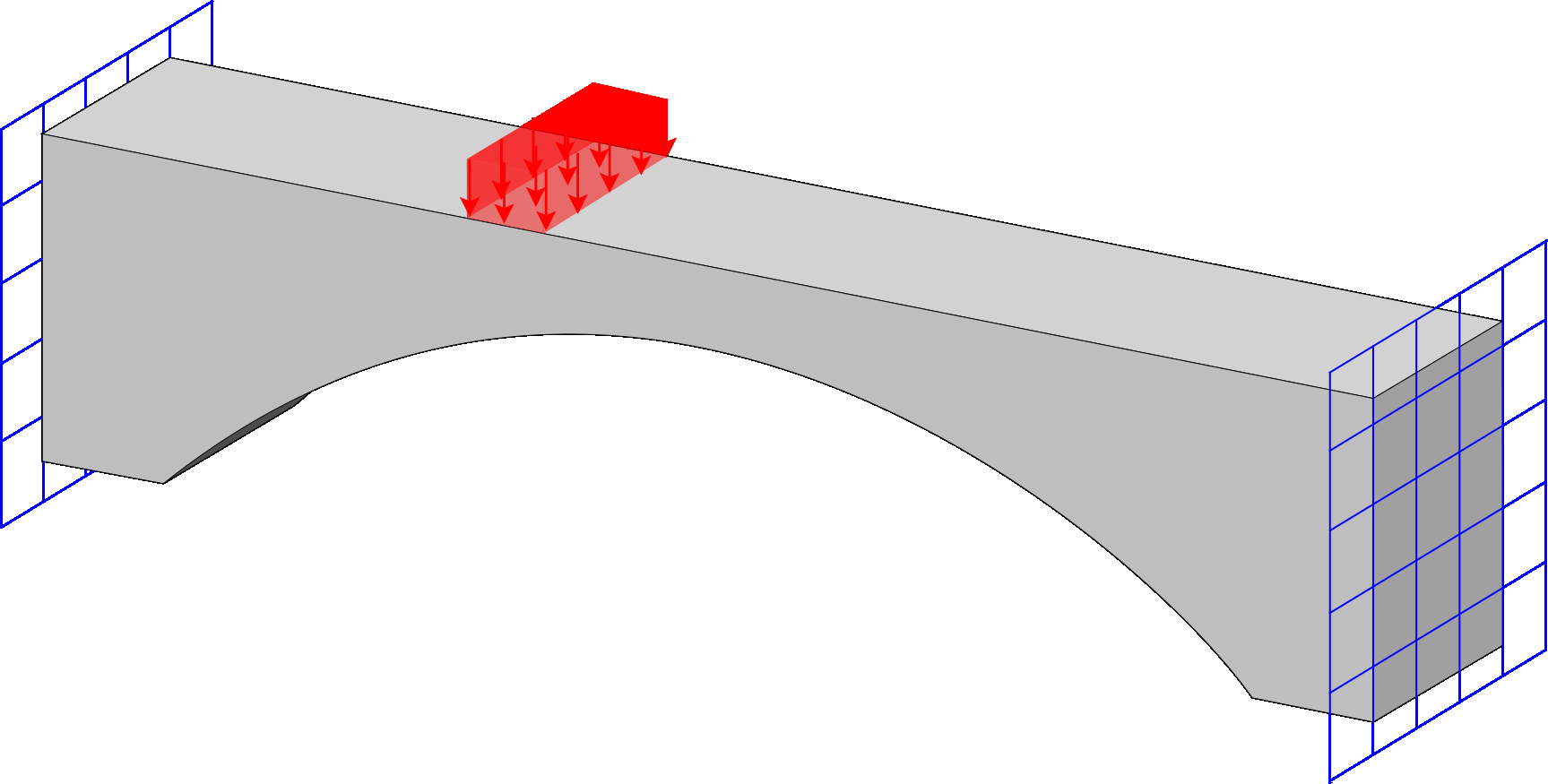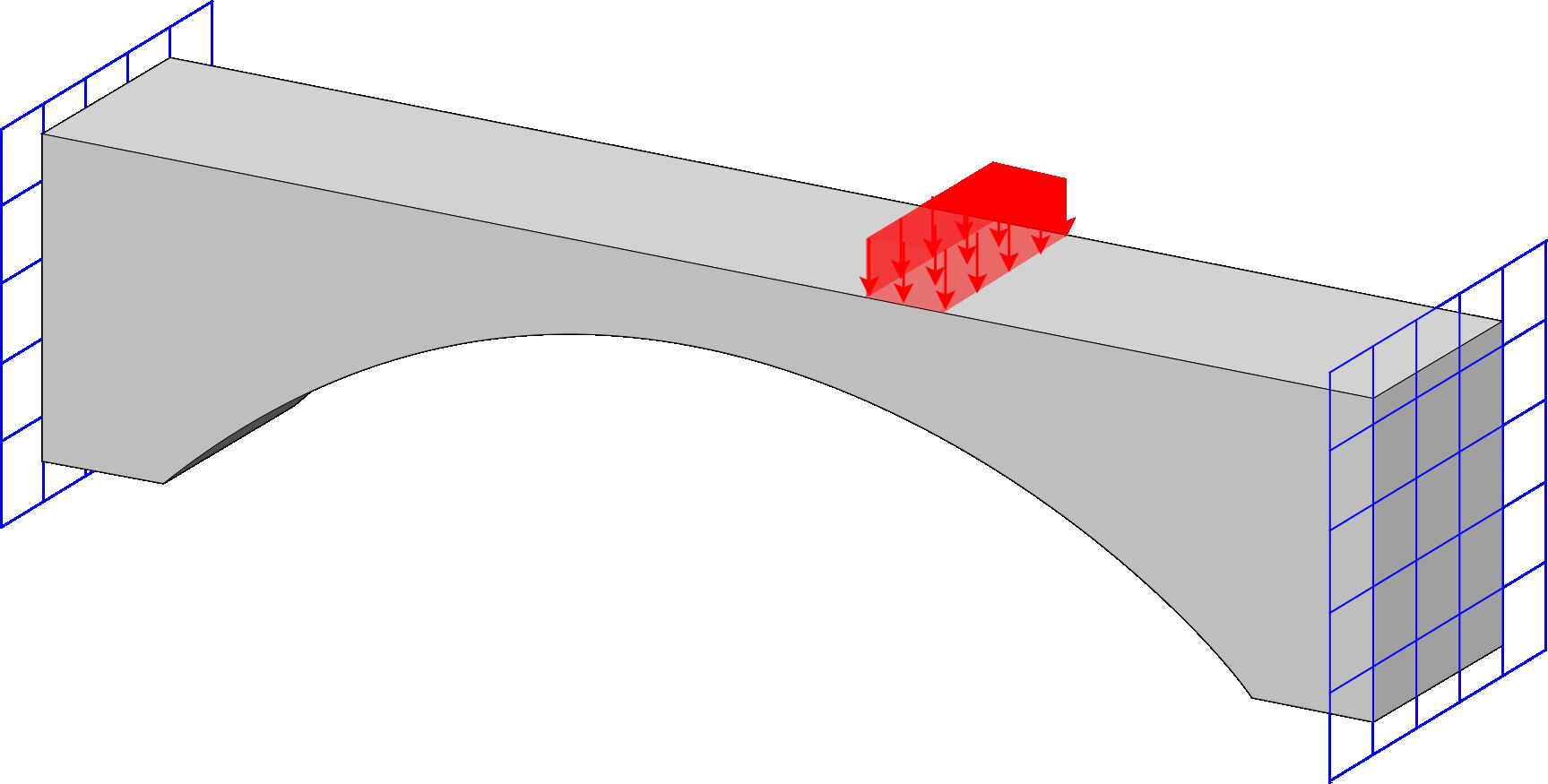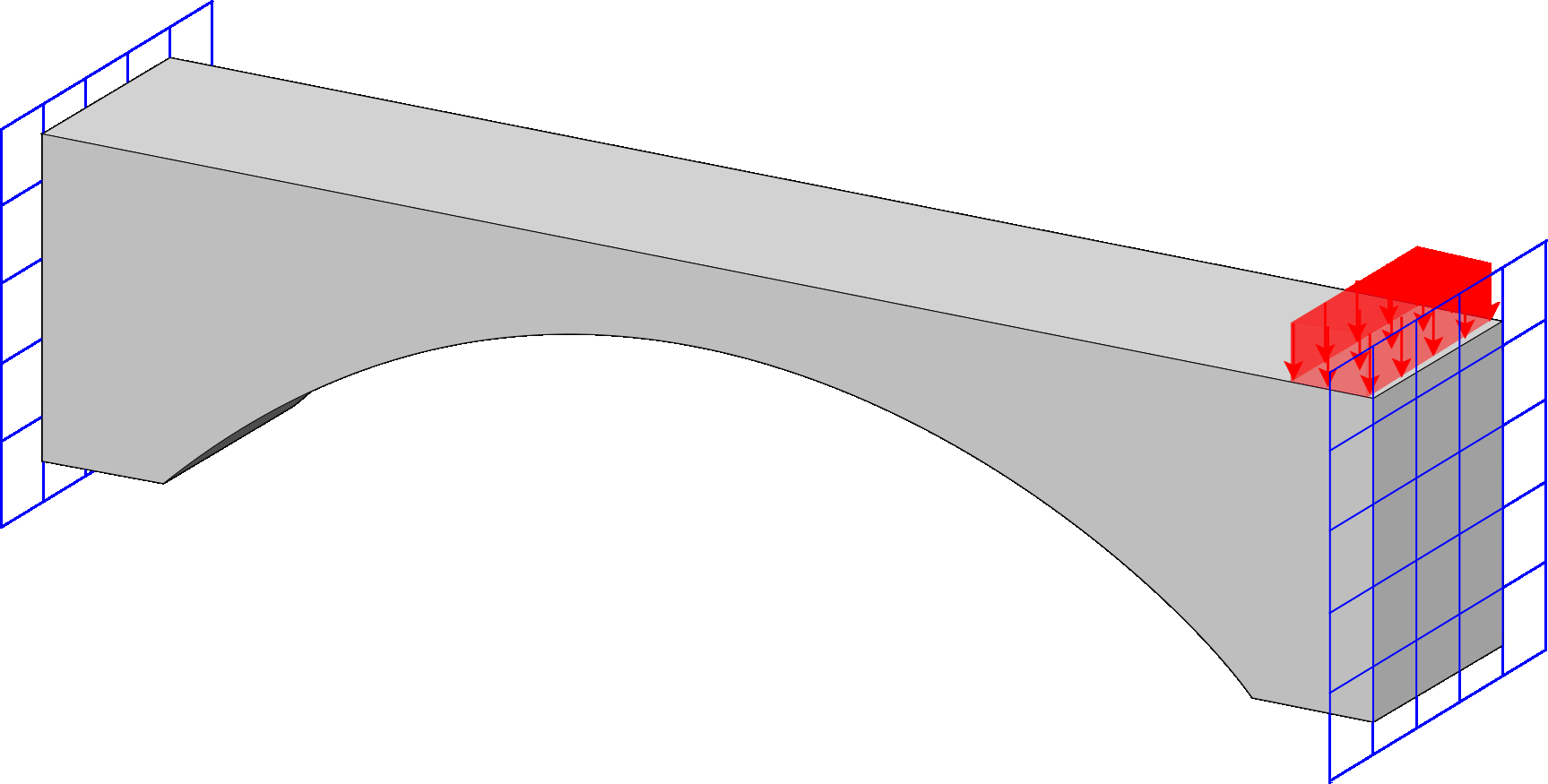

Spectrum Fem
Computational framework for response-spectrum analysis, incorporating both eigen and Ritz vectors methods, and the possibility of additional masses. It includes multiple response estimation techniques (modal combination formulas) to evaluate the structural response.
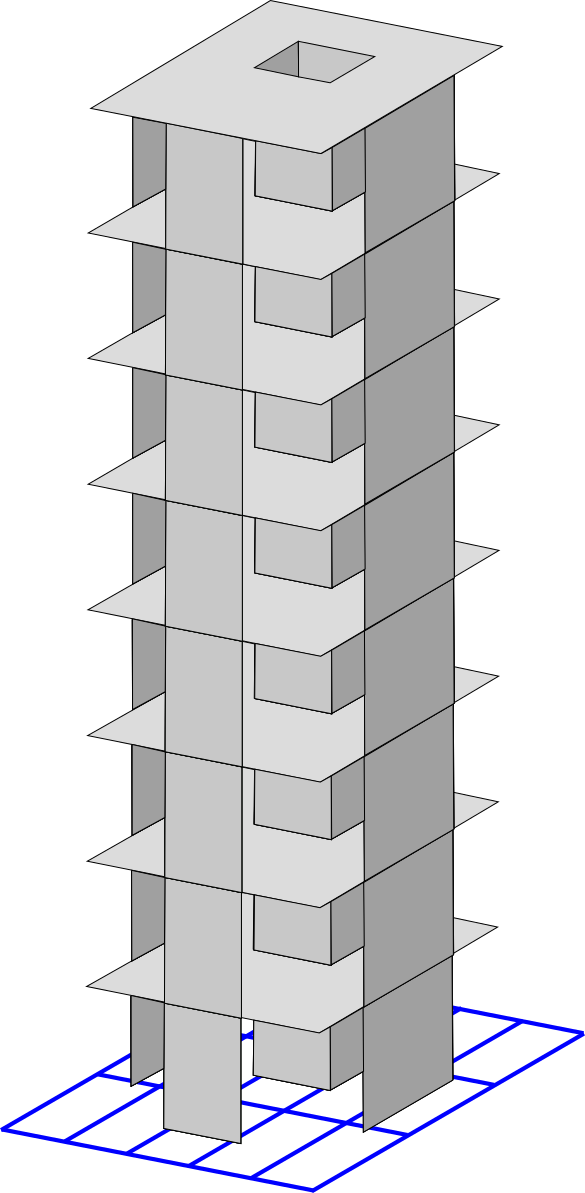
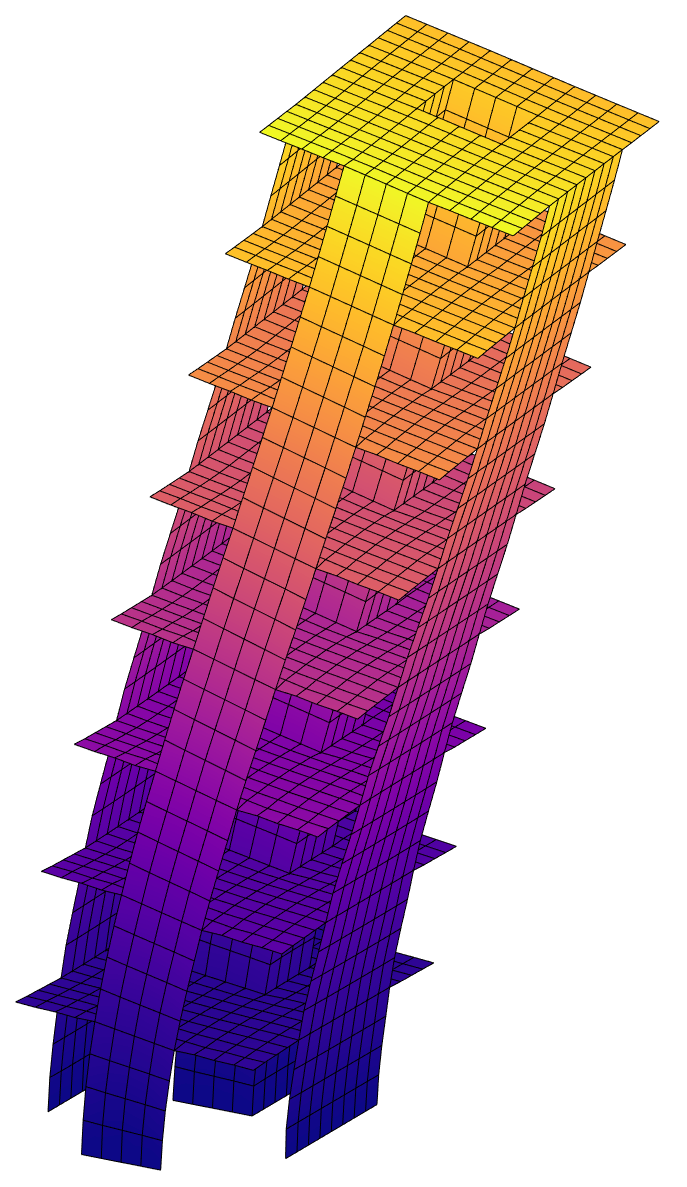
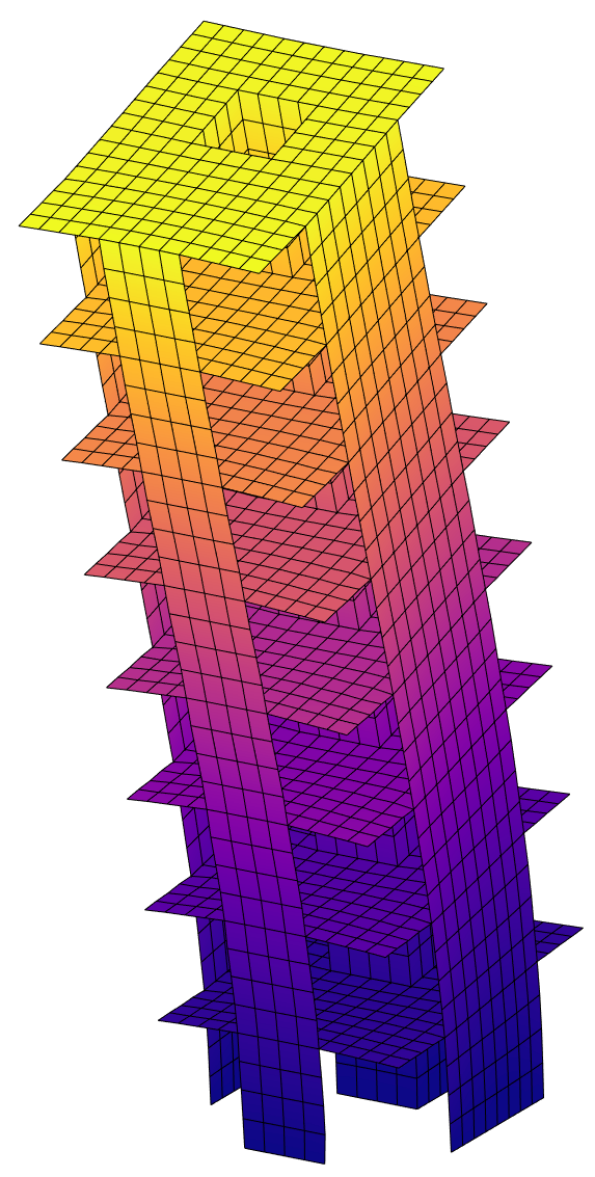
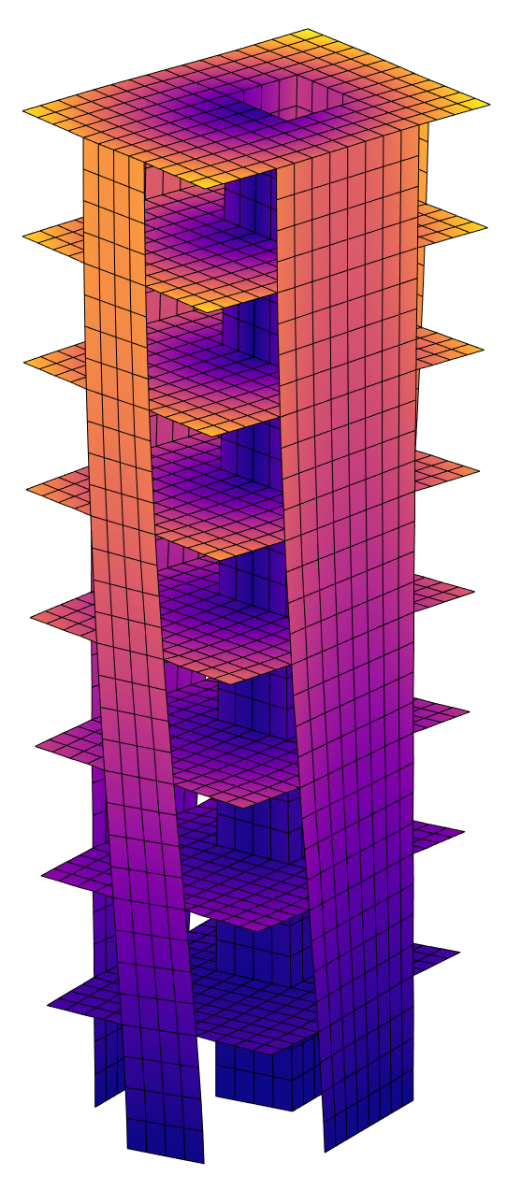
Development of topology-optimization frameworks spanning diverse applications, including classical topology optimization, shape optimization, optimization for multiple load cases, subdomain-selection approaches, multi-material formulations, optimization under dynamic loads, and stress-constrained optimization.
Top
Computational framework for topology optimization, supporting objectives such as compliance minimization and control-point displacement constraints. It includes different material-interpolation schemes, two- and three-field filtering techniques, various update schemes, and the option to use continuation for multiple parameters.
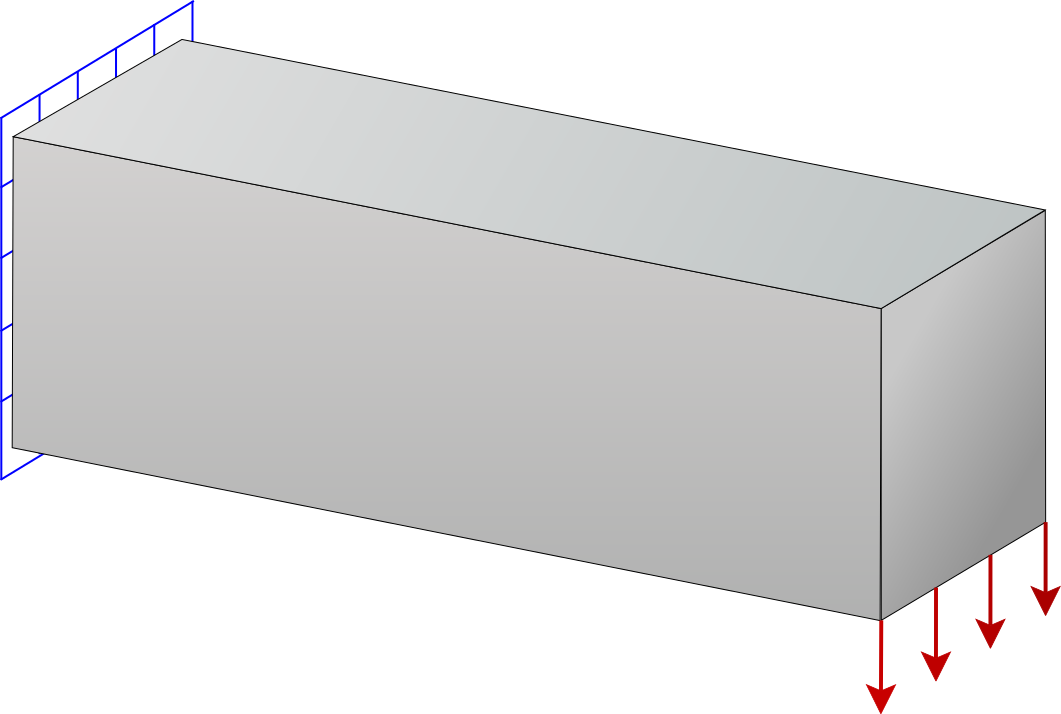

Shape Top
Computational framework for shape optimization, built on a constrained topology-optimization framework. This approach enables shape optimization directly on the structural domain, without the need to predefine a parametric boundary.
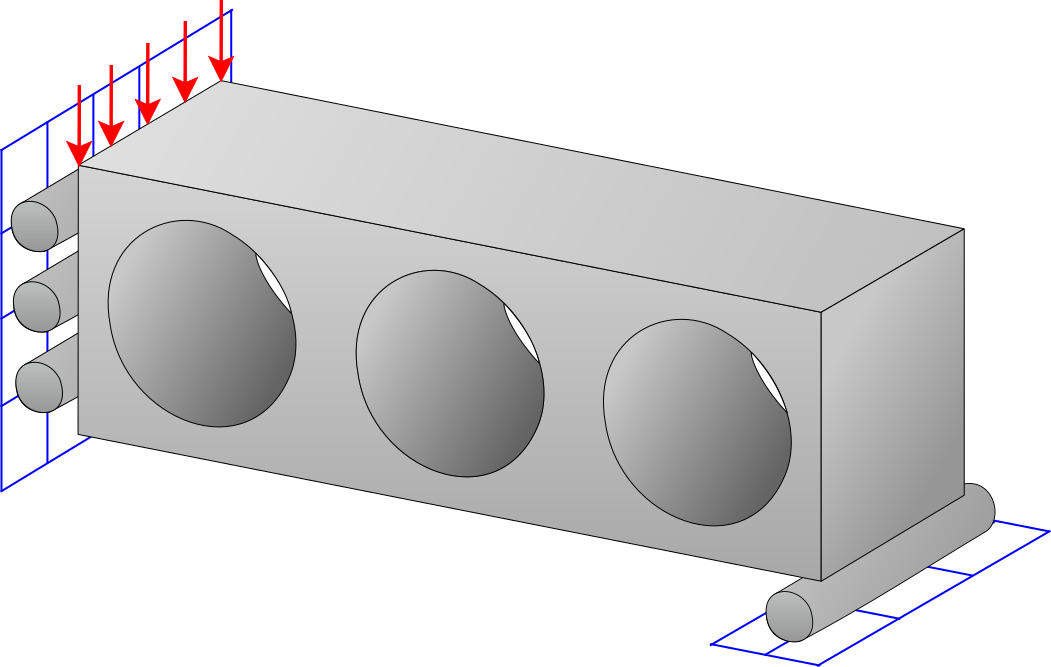

Multi Load Top
Computational framework for multi-load topology optimization. The implementation supports different methods for handling multiple loads and also provides the possibility of defining multiple objectives associated to each individual load case.
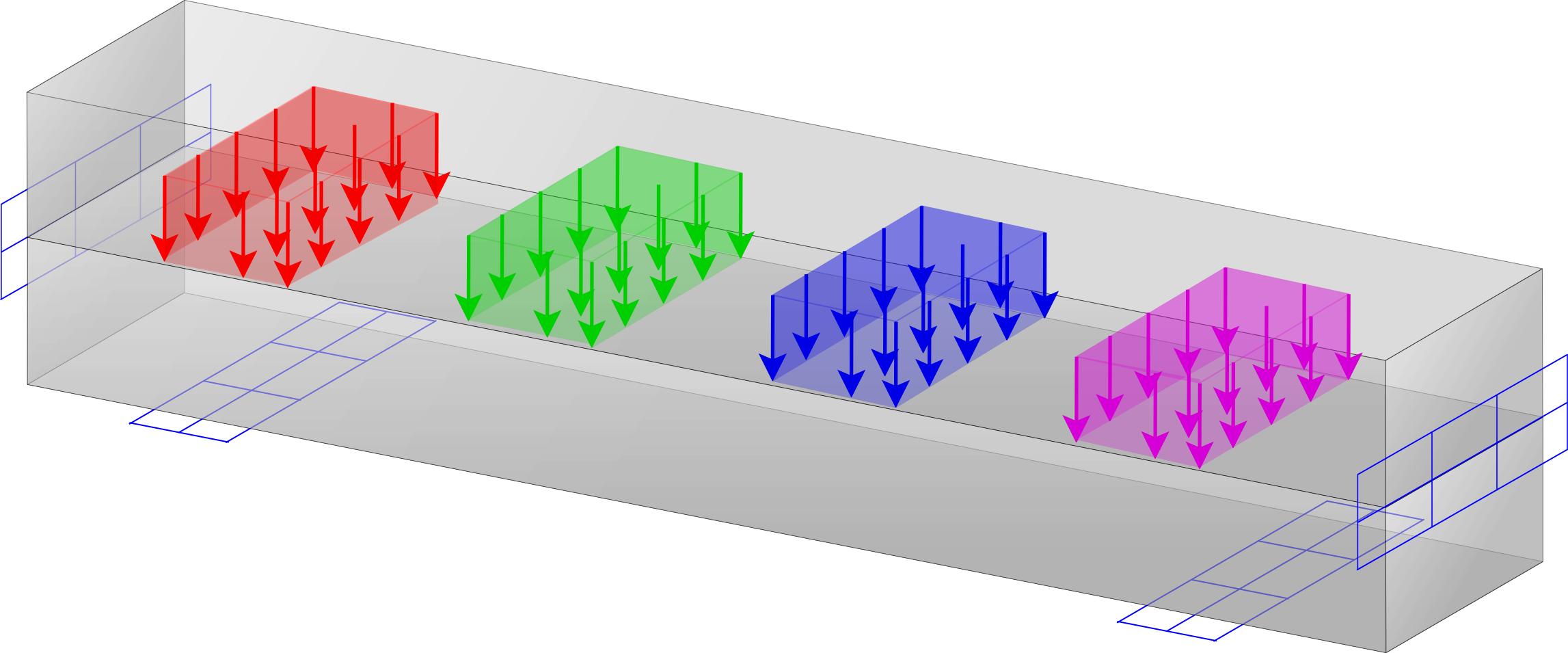

SubDomain Top
Computational framework for topology optimization with subdomain selection. The framework enables independent control of the global volume fraction, the number of active subdomains, and supports various material interpolation schemes for material densities as well as subdomain penalization.
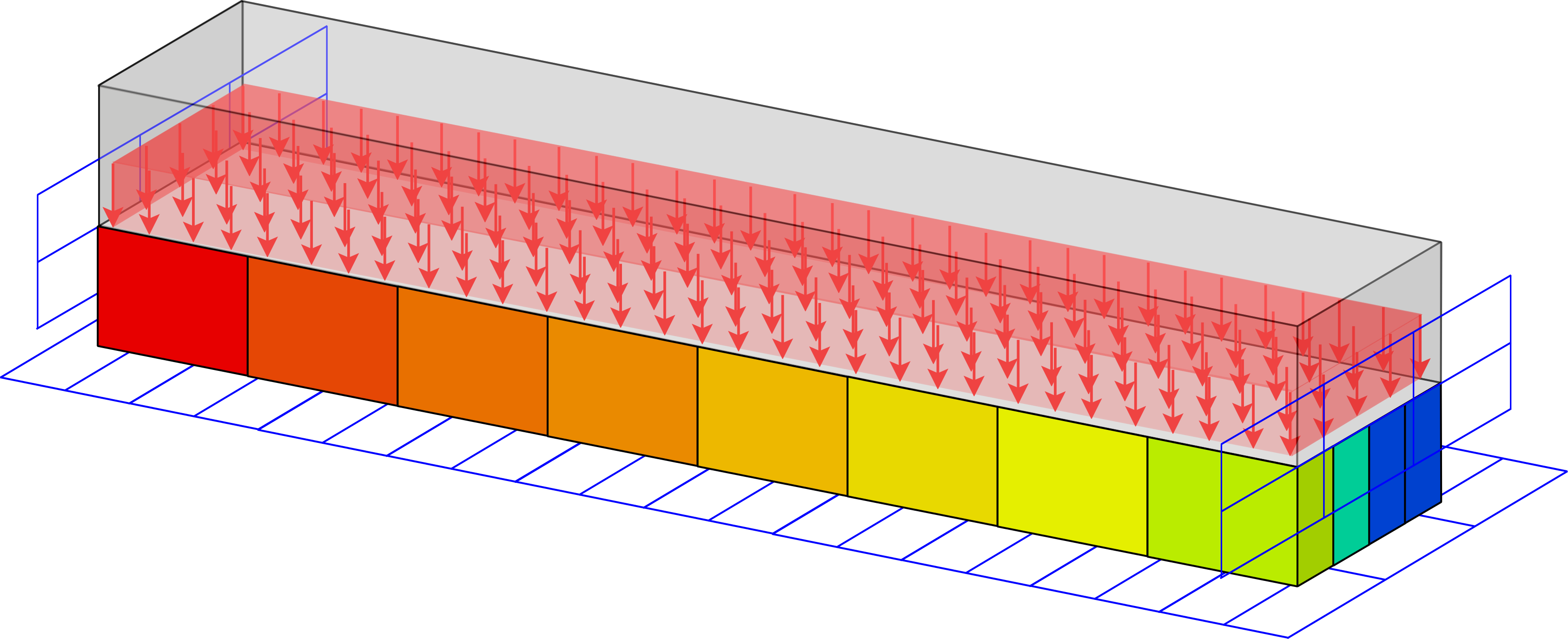

Multi Mat Top
Computational framework for multi-material topology optimization. The implementation allows assigning different material interpolation schemes, defining passive regions locked to a chosen material, and selecting among various update schemes.
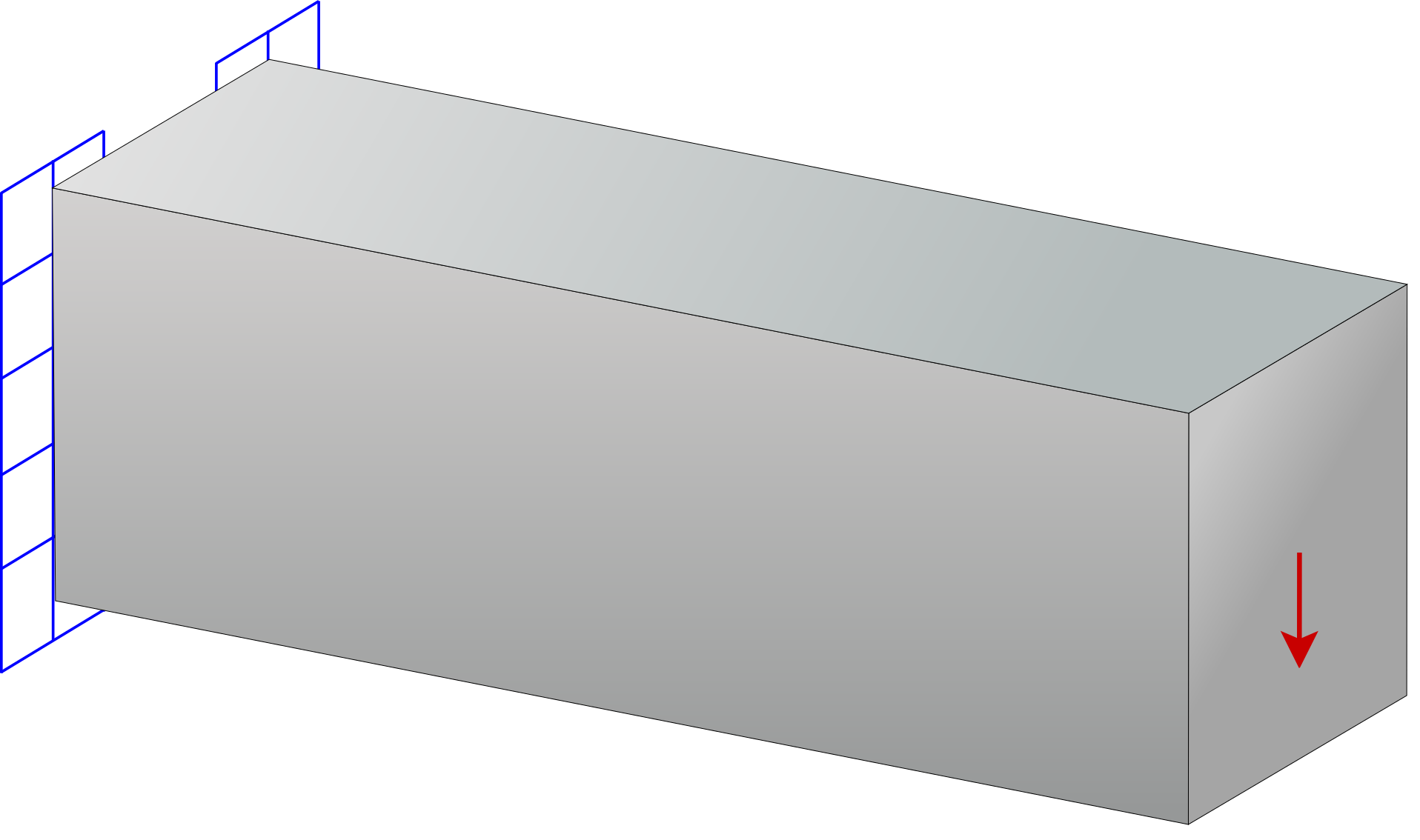

Dynamic Top
Computational framework for dynamic topology optimization. The implementation enables topology optimization under dynamic load cases derived from static patterns, dynamic patterns, and even ground motions. The framework supports optimization in both the time and frequency domains, with multiple methods available for each approach.
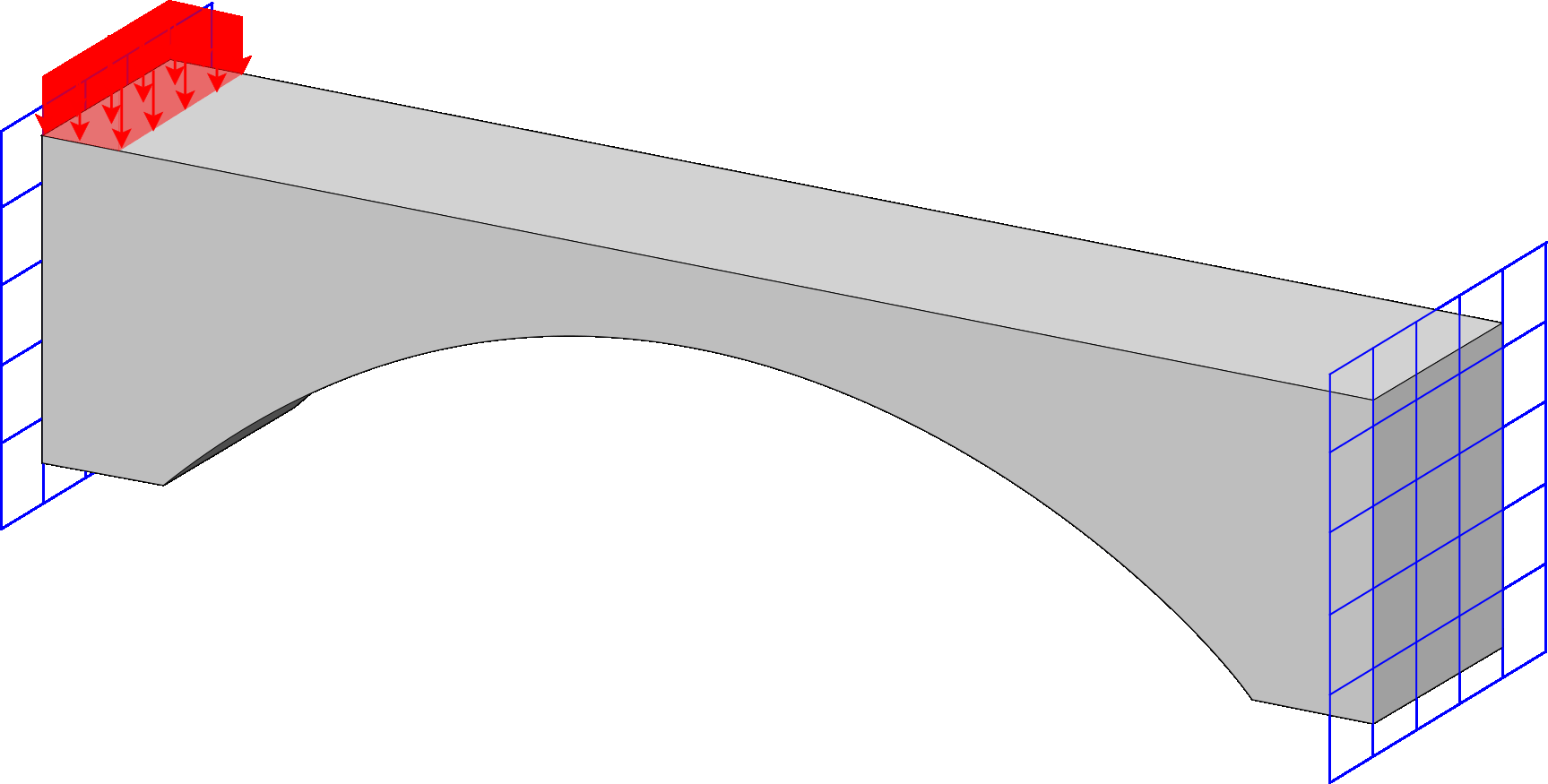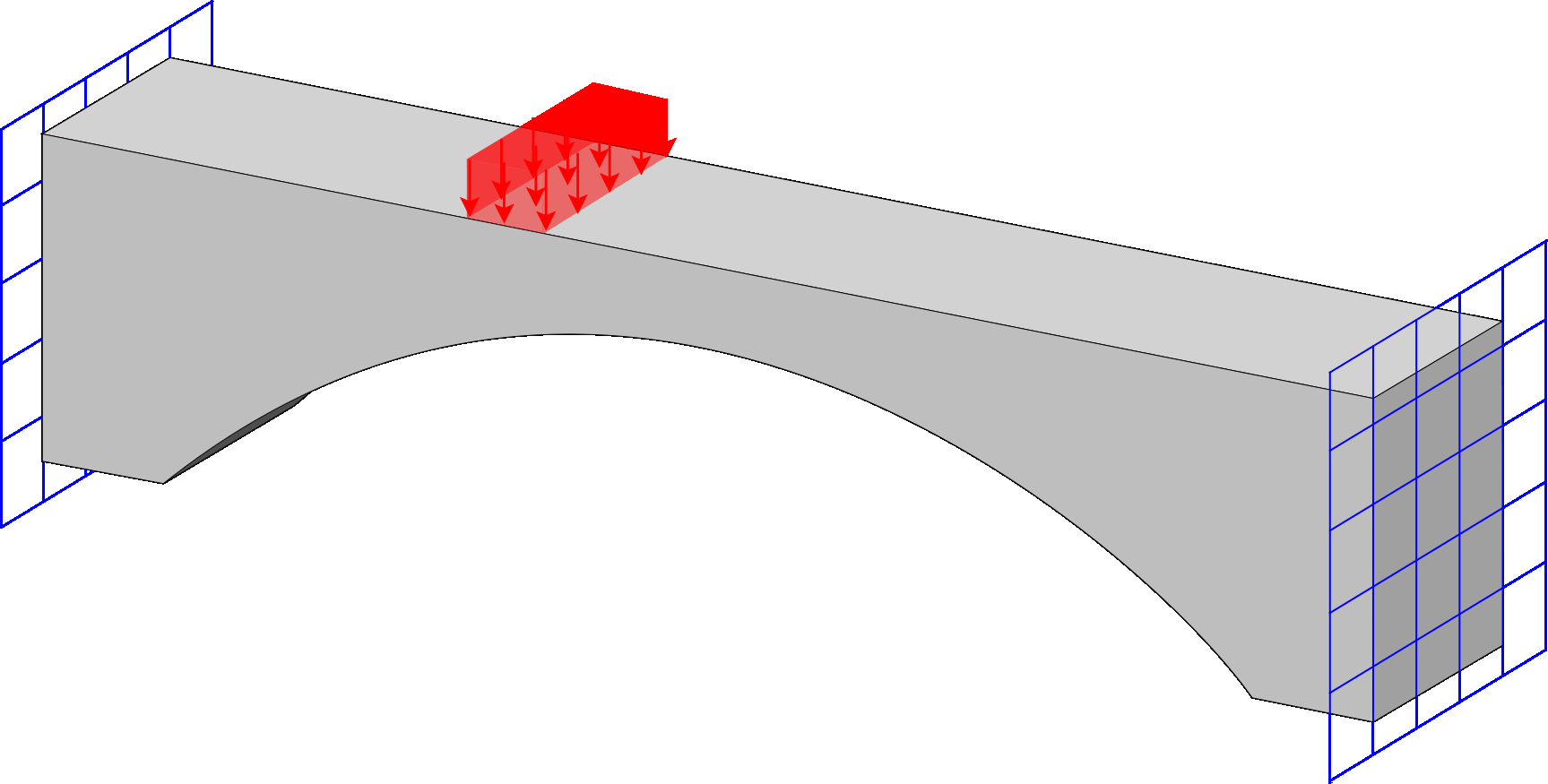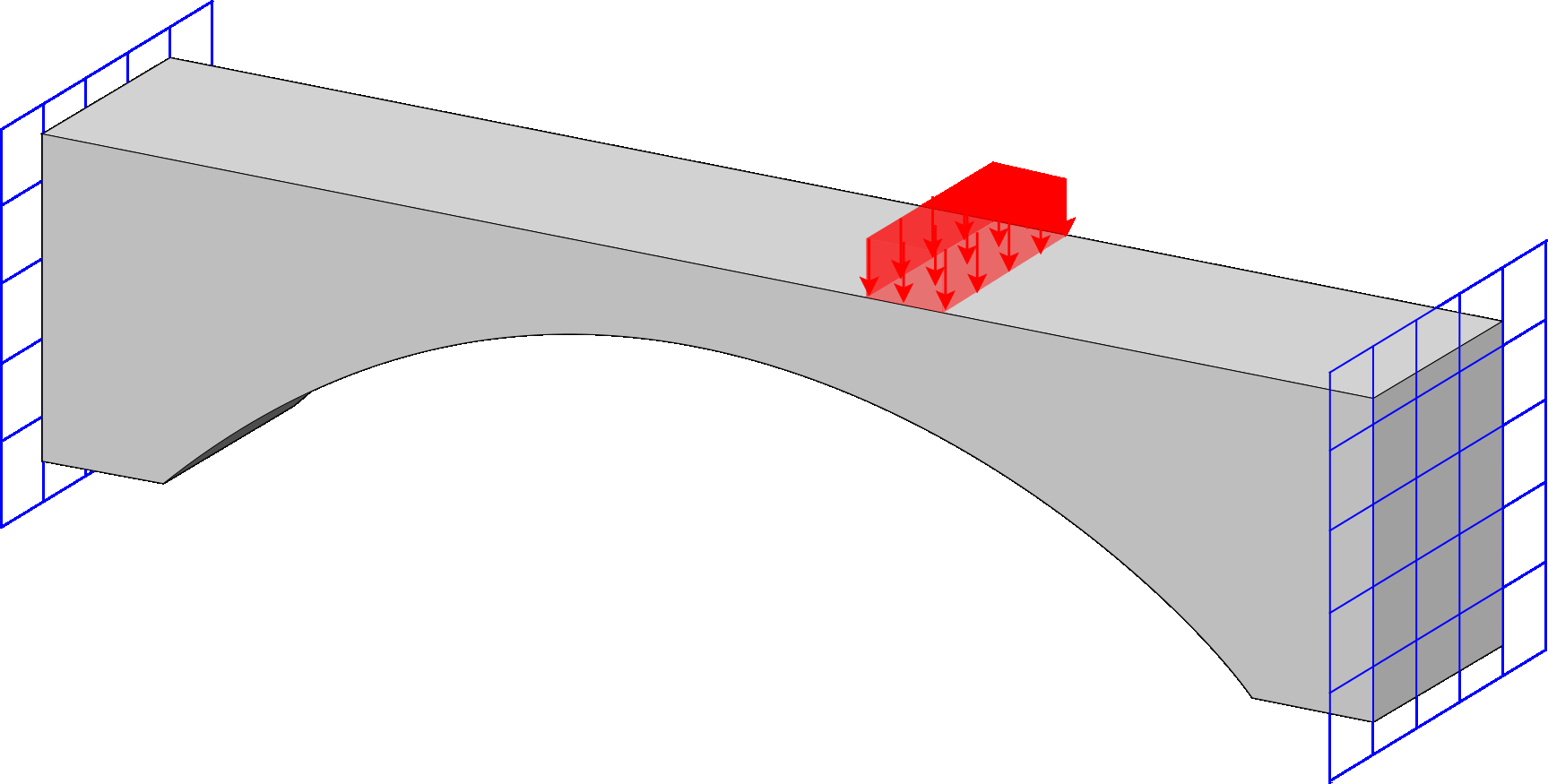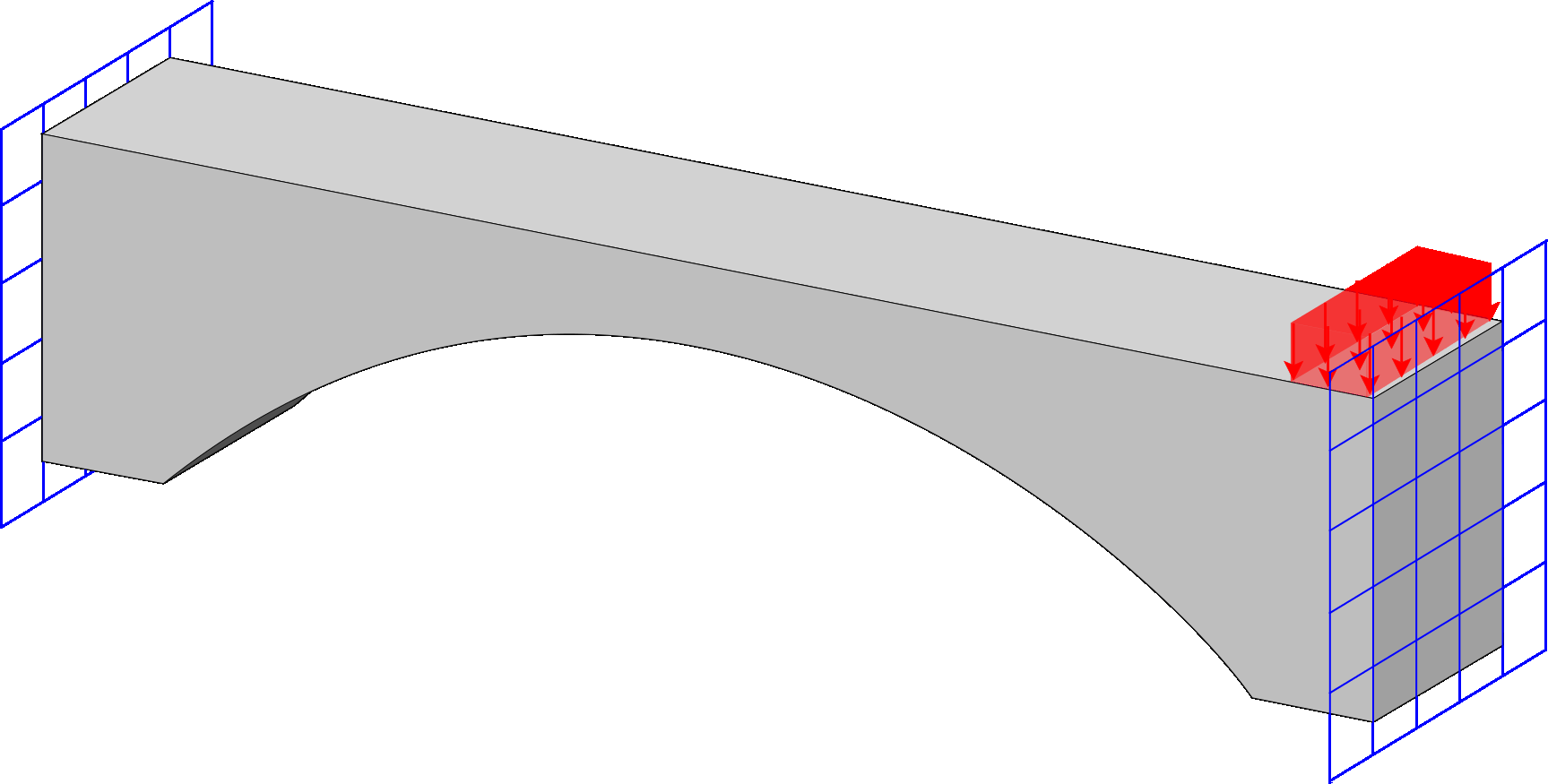

Stress Top
Computational framework for stress-constrained topology optimization. The implementation offers multiple techniques for handling vanishing constraints, and allows selection of the number of Gauss points at which stress constraints are enforced.
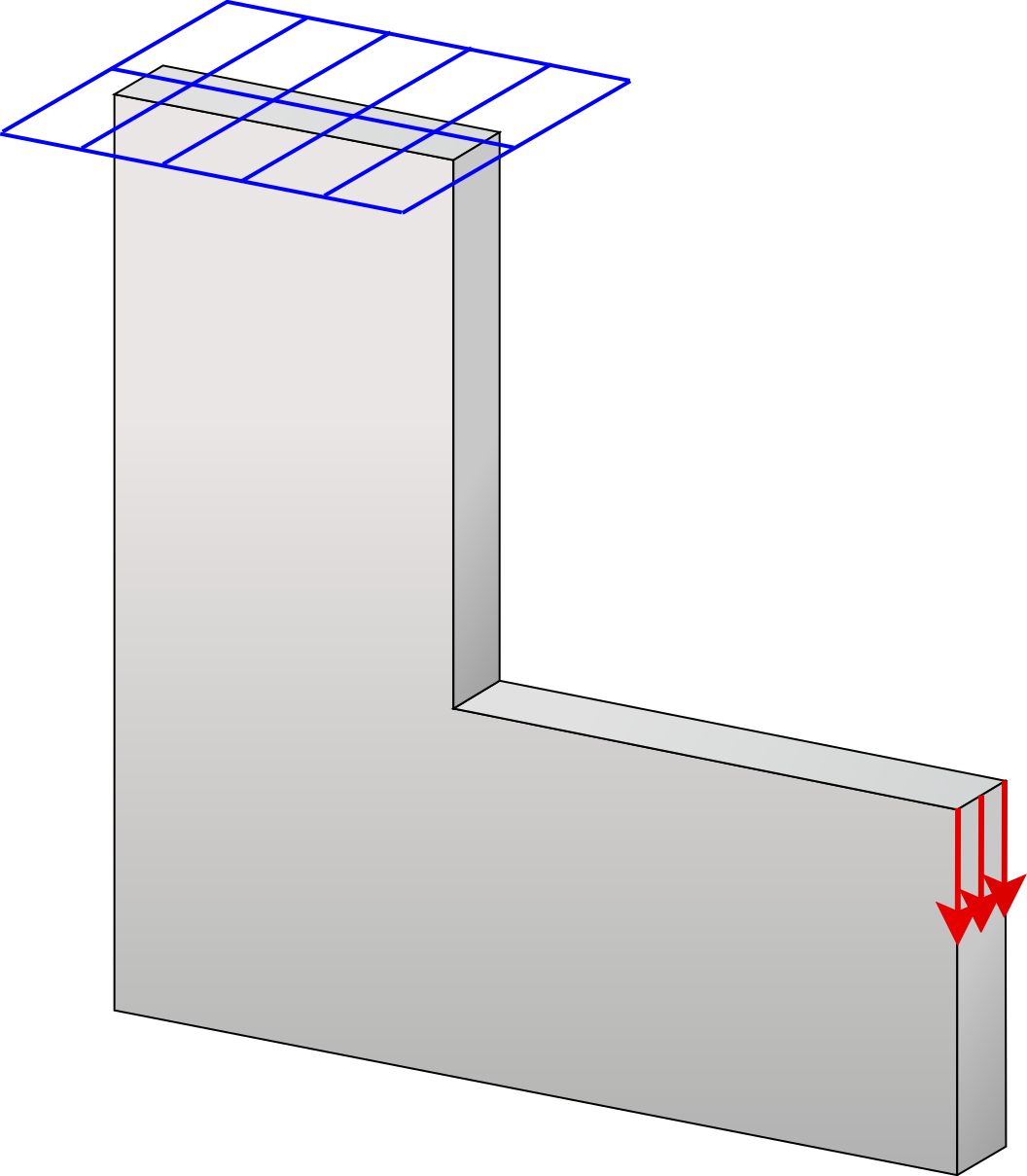
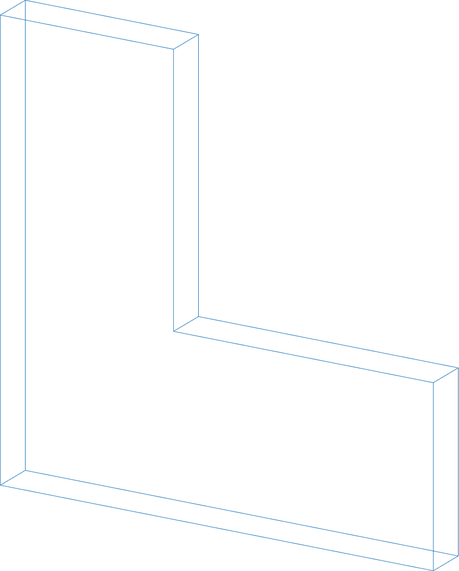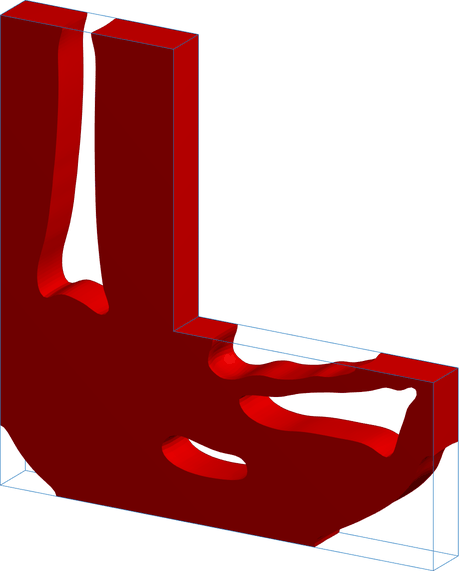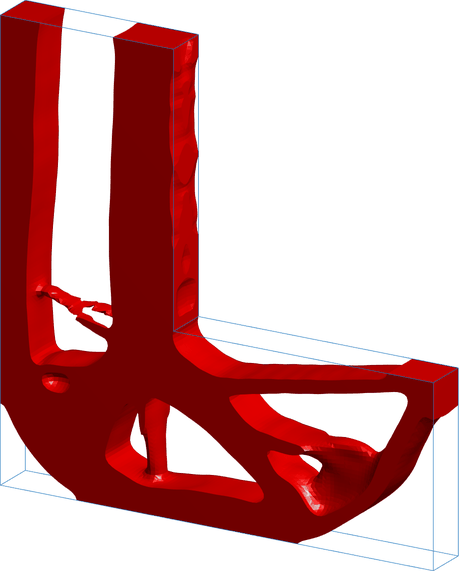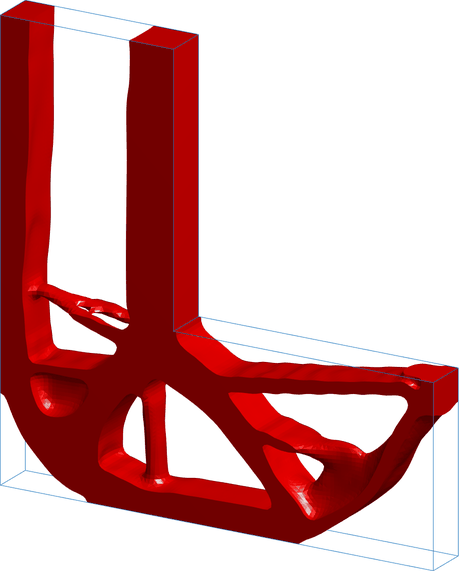
Comp Mech Top
Computational framework for compliant mechanism design using topology optimization. The implementation supports different objective formulations, including mechanical advantage maximization and control-point displacement maximization.

Multi Resolution Top
Computational framework for multi-resolution topology optimization. The implementation supports different refinement strategies and numerical integration schemes depending on the element types used.
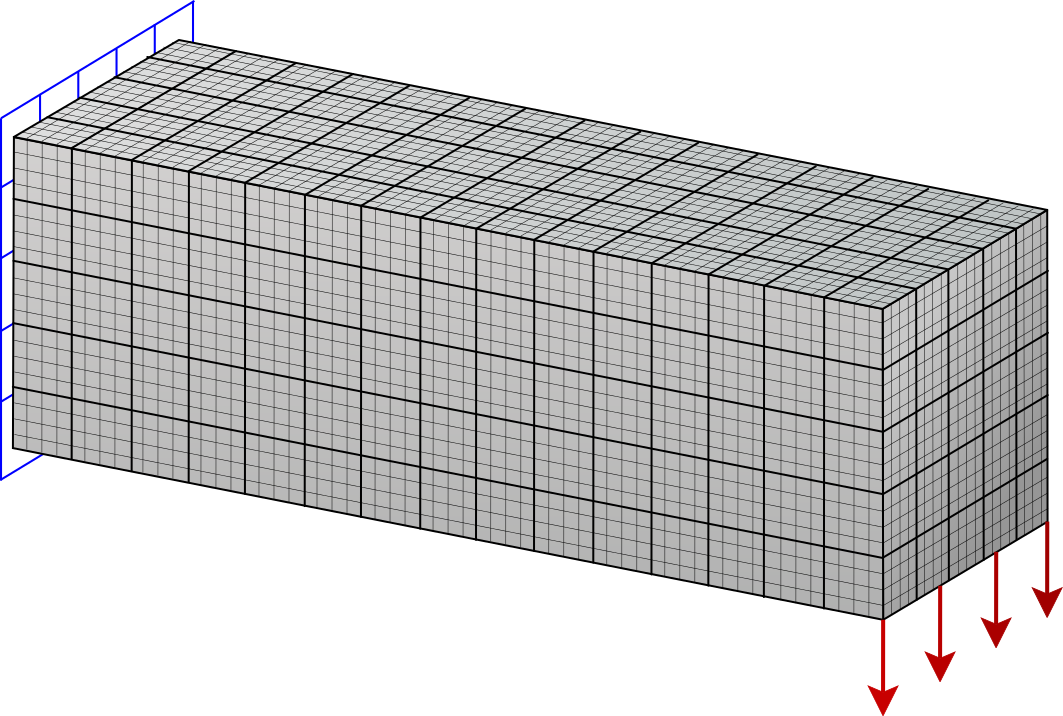

Development of geometry and meshing algorithms.
March
Computational framework for marching algorithms. These algorithms allow the computation of isosurfaces and isocaps for arbitrary domains and can be applied to different element types.


Development of topology optimization applications for applied engineering problems.
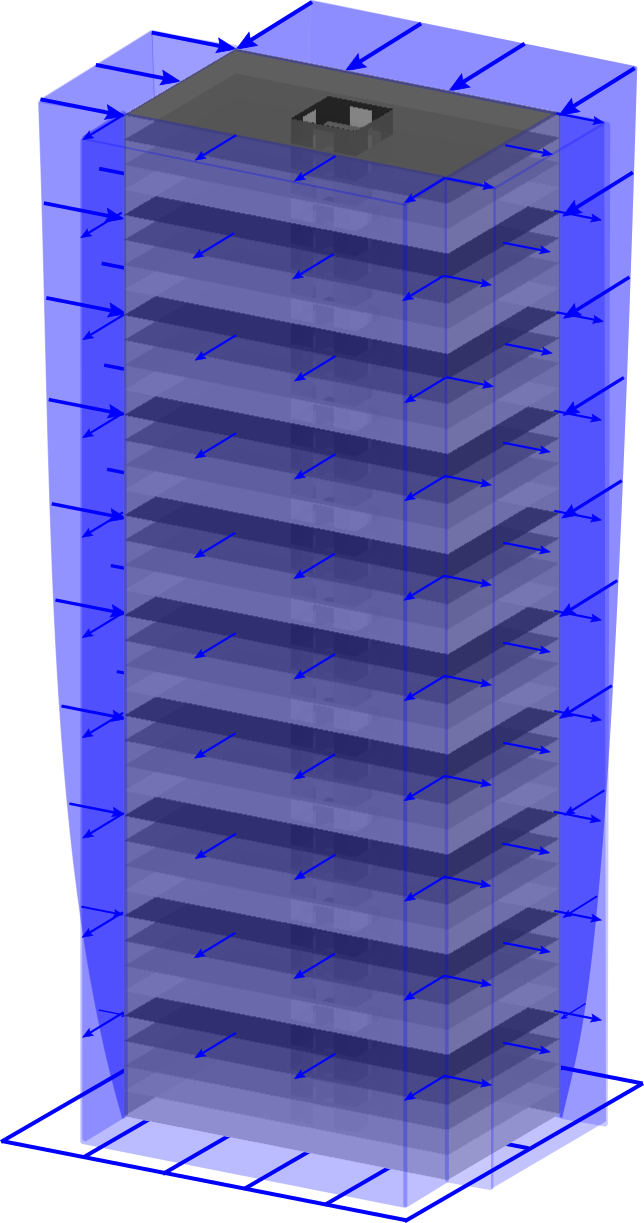
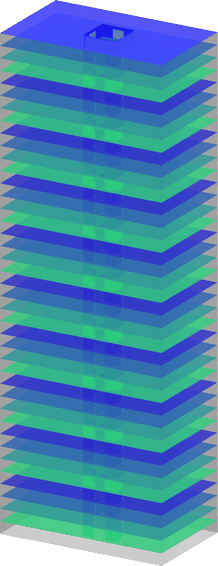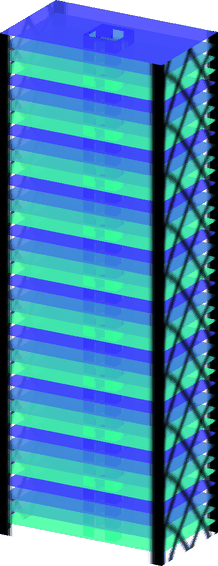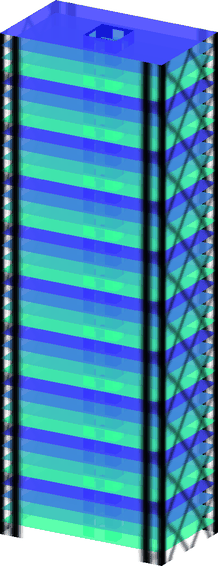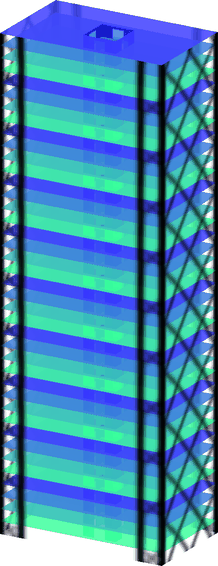
Building Wind Top
Computational framework for topology optimization of building facades subjected to static equivalent wind loads. It includes the use of pattern repetition and multi-objective optimization techniques.